题目内容
【题目】已知函数f(x)=|x﹣1|+|x+a|, ![]()
(1)当a=﹣2时,求不等式f(x)<g(x)的解集;
(2)若a>﹣1,且当x∈[﹣a,1]时,不等式f(x)≤g(x)有解,求实数a的取值范围.
【答案】
(1)解:当a=﹣2时,
f(x)=|x﹣1|+|x﹣2|= 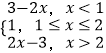 ,
,
∴f(x)<g(x)等价于 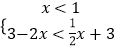 或
或 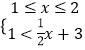 或
或 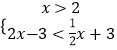 ,
,
解得0<x<1或1≤x≤2或2<x<4,即0<x<4.
∴不等式f(x)<g(x)的解集为{x|0<x<4}.
(2)解:∵x∈[﹣a,1],∴f(x)=1﹣x+x+a=a+1,
不等式f(x)=a+1≤g(x)max=( ![]() )max,
)max,
∴﹣1<a≤ ![]() ,
,
∴实数a的取值范围是(﹣1, ![]() ].
].
【解析】(1)当a=﹣2时,f(x)<g(x)等价于 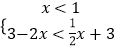 或
或 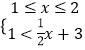 或
或 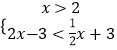 ,由此能求出不等式f(x)<g(x)的解集.(2)推导出f(x)=a+1,不等式f(x)≤a+1≤(
,由此能求出不等式f(x)<g(x)的解集.(2)推导出f(x)=a+1,不等式f(x)≤a+1≤( ![]() )max , 由此能求出实数a的取值范围.
)max , 由此能求出实数a的取值范围.

练习册系列答案
相关题目


