Question

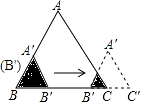
【题目】如图，已知∠AOB=a外有一点P，画点P关于直线OA的对称点P′，再作点P′关于直线OB的对称点P″．

（1）试猜想∠POP″与a的大小关系，并说出你的理由．

（2）当P为∠AOB 内一点或∠AOB边上一点时，上述结论是否成立？

Answer 1

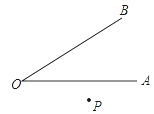
【答案】（1）∠POP″=2α （2）成立

【解析】

（1）根据轴对称的性质画出图形，再由直角三角形全等的判定定理得出：△DOP′≌△DOP，△EOP″≌△EOP′，根据全等三角形的性质即可得出结论．

（2）根据题意画出图形，同（1）可得出结论．

（1）猜想：∠POP″=2α．

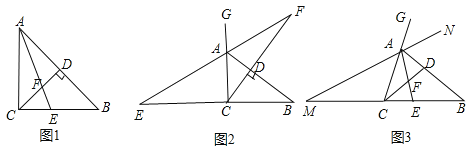
理由：如图1，在△DOP′与△DOP中

∵，

∴△DOP′≌△DOP．

同理可得，△EOP″≌△EOP′

∴∠POP″=2α；

（2）成立．

如图2，当点P在∠AOB内时，

∵同（1）可得，

△DOP′≌△DOP，EOP″≌△EOP′，

∴∠POD=∠P′OD，∠EOP″=∠EOP′，

∴∠POP″=∠P′OP″﹣∠POP′=3α﹣α=2α．

如图3，当点P在∠AOB的边上时，

∵同（1）可得△EOP″≌△EOP，

∴∠POP″=2α．