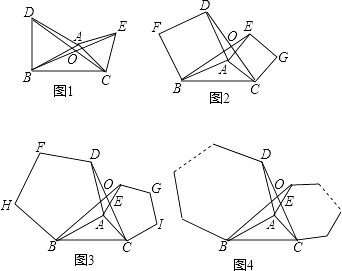
题目内容
【题目】小明在学习过程中,对教材中的一个有趣问题做如下探究:
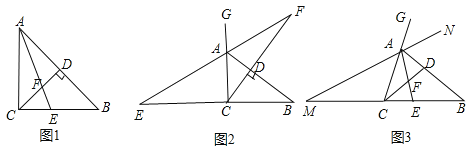
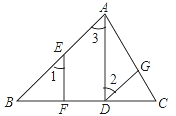
(习题回顾)已知:如图1,在△ABC中,∠ACB=90°,AE是角平分线,CD是高,AE、CD相交于点F.求证:∠CFE=∠CEF;
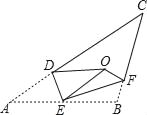
(变式思考)如图2,在△ABC中,∠ACB=90°,CD是AB边上的高,若△ABC的外角∠BAG的平分线交CD的延长线于点F,其反向延长线与BC边的延长线交于点E,则∠CFE与∠CEF还相等吗?说明理由;
(探究廷伸)如图3,在△ABC中,在AB上存在一点D,使得∠ACD=∠B,角平分线AE交CD于点F.△ABC的外角∠BAG的平分线所在直线MN与BC的延长线交于点M.试判断∠M与∠CFE的数量关系,并说明理由.
【答案】【习题回顾】证明见解析;【变式思考】∠CEF=∠CFE,理由见解析;【探究思考】∠M+∠CFE=90°,理由见解析.
【解析】
根据三角形的外角的性质证明;
【变式思考】
根据角平分线的定义、直角三角形的性质解答;
【探究廷伸】
同(1)、(2)的方法相同.
∵∠ACB=90°,CD是高,∴∠B+∠CAB=90°,∠ACD+∠CAB=90°,∴∠B=∠ACD.
∵AE是角平分线,∴∠CAF=∠DAF.
∵∠CFE=∠CAF+∠ACD∠CEF=∠DAF+∠B,∴∠CEF=∠CFE;
变式思考:∠CEF=∠CFE.证明如下:
∵AF为∠BAG的角平分线,∴∠GAF=∠DAF.
∵CD为AB边上的高,∴∠ACB=90°,∴∠ADF=∠ACE=90°.
又∵∠CAE=∠GAF,∴∠CEF=∠CFE;
探究思考:∠M+∠CFE=90°.证明如下:
∵C、A、G三点共线 AE、AN为角平分线,∴∠EAN=90°.
又∵∠GAN=∠CAM,∴∠MAE=90°,∴∠M+∠CEF=90°.
∵∠CEF=∠EAB+∠B,∠CFE=∠EAC+∠ACD,∠ACD=∠B,∴∠CEF=∠CFE,∴∠M+∠CFE=90°.