题目内容
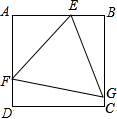
如图，正△EFG内接于正方形ABCD，其中E，F，G分别在边AB，AD，BC上，若
=2，则
=______．
| AE |
| EB |
| BG |
| BC |
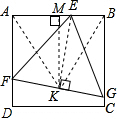
如图，作EK⊥FG，K是FG的中点，连AK、KB，易知E、K、G、B和E、K、F、A分别四点共圆
∴∠KBE=∠EGK=60°，∠EAK=∠EFK=60°．
∴三角形ABK是等边三角形
作KM⊥AB，M是AB的中点，设AB=6
则EB=
AB=2，MB=3，ME=1，MK=6sin60°=3
∴EK=
=2
；
EG=
=
；
BG=
=
．
故
=
．
故答案为
．
∴∠KBE=∠EGK=60°，∠EAK=∠EFK=60°．
∴三角形ABK是等边三角形
作KM⊥AB，M是AB的中点，设AB=6
则EB=
| 1 |
| 3 |
| 3 |
∴EK=
| ME2+MK2 |
| 7 |
EG=
| EK |
| sin60° |
4
| ||
| 3 |
BG=
| EG2-BE2 |
10
| ||
| 3 |
故
| BG |
| BC |
5
| ||
| 9 |
故答案为
5
| ||
| 9 |
练习册系列答案
小学教材完全解读系列答案
相关题目
