题目内容
已知在△ABC中,∠C=90°,AB=12,点G为△ABC的重心,那么CG= .
4.
试题分析:在Rt△ABC中,∠C=90°,点G为重心,AB=12,则AB边上的中线是6,根据重心的性质即可求出CG.
在Rt△ABC中,∠C=90°,
∵AB=12,
∴AB边上的中线是6,
∵点G为重心,
∴CG=6×
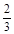 =4.
=4.故答案是:4.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
题目内容
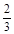 =4.
=4.
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案