题目内容
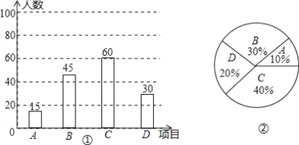
【题目】为推广阳光体育“大课间”活动,某中学决定在学生中开设A:实心球,B:立定跳远,C:跳绳,D:跑步四种活动项目.为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图.请结合图中的信息解答下列问题:
(1)在这项调查中,共调查了多少名学生?
(2)请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两幅统计图中的B补充完整;
(3)若调查到喜欢“跳绳”的5名学生中有3名男生,2名女生.现从这5名学生中任意抽取2名学生.请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.
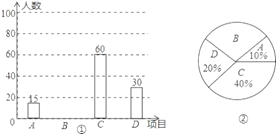
【答案】(1)在这项调查中,共调查了150名学生;
(2)喜欢“立定跳远”的学生人数为45人,“立定跳远”的学生占被调查学生的30%;补全图形见解析;
(3)刚好抽到同性别学生的概率是![]() .
.
【解析】试题分析:(1)用A的人数除以所占的百分比,即可求出调查的学生数;(2)用抽查的总人数减去A、C、D的人数,求出喜欢“立定跳远”的学生人数,再除以被调查的学生数,求出所占的百分比,再画图即可;(3)用A表示男生,B表示女生,画出树形图,再根据概率公式进行计算即可.
试题解析:(1)根据题意,得:15÷10%=150(人),
答:在这项调查中,共调查了150名学生;
(2)本次调查中喜欢“立定跳远”的学生人数为:150﹣15﹣60﹣30=45(人),
“立定跳远”的学生占被调查学生百分比为: ![]() ×100%=30%,
×100%=30%,
补全图形如下:
(3)用A表示男生,B表示女生,画图如下:

共有20种情况,同性别学生的情况是8种,则刚好抽到同性别学生的概率是![]() =
=![]() .
.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目