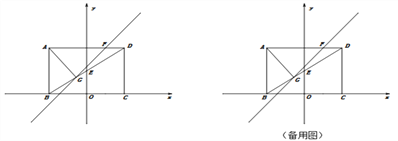题目内容
【题目】如图,在Rt△ABC中,∠ACB=90,AC=3,BC=4,分别以AB、AC、BC为边在AB同侧作正方形ABEF,ACPQ,BDMC,记四块阴影部分的面积分别为S1、S2、S3、S4 , 则S1+S2+S3+S4= . 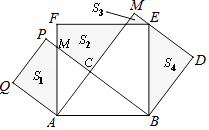
【答案】18
【解析】解:过F作AM的垂线交AM于N, 则Rt△ANF≌Rt△ABC,Rt△NFK≌Rt△CAT,
所以S2=SRt△ABC .
由Rt△NFK≌Rt△CAT可得:Rt△FPT≌Rt△EMK,
∴S3=S△FPT ,
可得Rt△AQF≌Rt△ACB,
∴S1+S3=SRt△AQF=SRt△ABC .
∵Rt△ABC≌Rt△EBD,
∴S4=SRt△ABC
∴S1+S2+S3+S4
=(S1+S3)+S2+S4
=SRt△ABC+SRt△ABC+SRt△ABC
=SRt△ABC×3
=4×3÷2×3
=18.
所以答案是:18.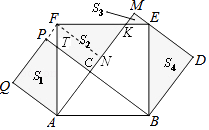
【考点精析】根据题目的已知条件,利用勾股定理的概念的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目