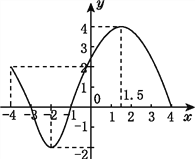
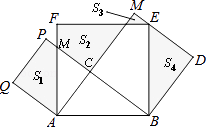
题目内容
【题目】如图,已知A,D,E三点共线,C,B,F三点共线,AB=CD,AD=CB,DE=BF,那么BE与DF之间有什么数量关系?请说明理由.
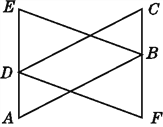
【答案】答案见解析
【解析】试题分析: 连接BD,由SSS可证明△ABD≌△CDB,从而得到∠A=∠C,再由AD=CB,DE=BF,得到AE=CF,即可证明△ABE≌△CDF,由全等三角形的性质即可得出结论.
试题解析:解:BE=DF.理由如下:
如图,连接BD.
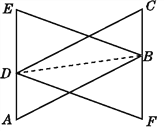
在△ABD和△CDB中, ∵AB=CD,AD=CB,BD=DB,∴△ABD≌△CDB(SSS),∴∠A=∠C.
∵AD=CB,DE=BF,∴AD+DE=CB+BF,∴AE=CF.
在△ABE和△CDF中,∵AE=CF,∠A=∠C,AB=CD,∴△ABE≌△CDF(SAS).∴BE=DF.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】下表是橘子的卖钱额随橘子卖出质量的变化表:
质量/千克 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
卖钱额/元 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 |
(1)在这个表中反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用x表示橘子的卖出质量,y表示卖钱额,按表中给出的关系,用一个式子把y与x之间的关系表示出来;
(3)当橘子卖出50千克时,预测卖钱额是多少?