题目内容
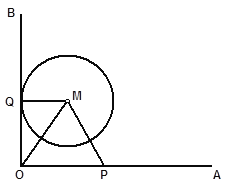
【题目】如图,射线OA⊥射线OB,半径![]() 的动圆M与OB相切于点Q,( 圆M 与OA没有公共点 ), P是OA上的动点,且PM
的动圆M与OB相切于点Q,( 圆M 与OA没有公共点 ), P是OA上的动点,且PM![]() .设OP=
.设OP= ![]()
![]() ,OQ=
,OQ= ![]()
![]() .
.
(1)求![]() 、
、![]() 所满足的关系式,并写出
所满足的关系式,并写出![]() 的取值范围 ;
的取值范围 ;
(2)当△MOP为等腰三角形时,求相应![]() 的值;
的值;
(3)是否存在大于2的实数![]() ,使△MQO∽△OMP?若存在,求相应
,使△MQO∽△OMP?若存在,求相应![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在
;(3)存在![]() ,使△MQO∽△MOP
,使△MQO∽△MOP
【解析】试题分析:(1)过点M作MD⊥OA,垂足为D,可以知道△MDP为直角三角形,DP=(x-2)cm,MD=ycm,勾股定理即可得出x、y所满足的关系式,并写出x的取值范围;(2)若△MOP为等腰三角形,①若OM=MP,则有OD=PD,此时x=2×2=4;②若MP=OP时,x=3;③若OM=OP时,OM=4+y2,结合(1)求出x的值;(3)△MQO∽△OMP,因为∠Q=90°,∠OMP=90°,根据相似比及(1)的关系式求相应x的值.
试题解析: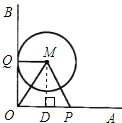
(1)过点M作MD⊥OA,垂足为D,显然ODMQ为矩形,
∴OD=MQ=2,MD=OQ=y,
∴PD=x2,
在Rt△MDP中,y2+(x2)2=32,
∴x24x+y2=5,
当如图所示情况时,OD=2;
当M与OA相切时,
可知OP=2+![]() ,
,
∴x取值范围为0x<2+![]() ;
;
(2)①若OM=MP,此时x=4,
②若MP=OP时,此时x=3,
③若OM=OP时,
∵OM=4+y2,
∴4+y2=x2,
∴![]() ,
,
解得x=![]() ;
;
(3)∵△QMO∽△MOP,此时∠OMP=90°,则![]() ,
,
∴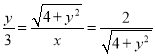 ,
,
∴4+y2=2x,
∴![]() ,
,
∴x=1+![]() <2
<2![]() ,
,
∴存在这样的实数x,并且x=1+![]() .
.

练习册系列答案
相关题目