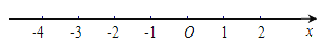题目内容
【题目】已知数轴上A、B两点对应的数分别为﹣2和8，P为数轴上任意一点且对应的数为x，C为线段PA的中点．
（1）若点P在线段AB上，求2BC﹣BP的值；
（2）若点P在线段AB的延长线上，式子2BC﹣BP的值是定值吗？若是，求出它的值，若不是，请说明理由．
【答案】（1）10；（2）是定值，值为10
【解析】
（1）表示出点C所表示的数，再表示出两点之间的距离，进而做出结果；
（2）分两种情况进行解答，一种是中点C在点B的左侧，另一种是点C在点B的右侧，分别画出相应的图形，利用数轴上的数表示两点之间的距离．
解：（1）如图1，设C点对应的数为c，
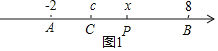
∵点P在线段AB上，C为线段PA的中点．
∴AC＝PC，
即：c+2＝x﹣c，
∴c＝
，
∴2BC﹣PB＝
＝10，
答：2BC﹣BP的值为10．
（2）∵点P在线段AB的延长线上，C为线段PA的中点．
∴AC＝PC，
即：c+2＝x﹣c，
∴c＝，
①若点C在点B左侧，如图2，
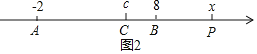
∴2BC﹣PB＝＝26﹣2x，
因此，当点C在点B左侧时2BC﹣BP的值不是定值；
②若点C在点B右侧，如图3，
∴2BC﹣PB＝＝10，
因此，当点C在点B右侧时2BC﹣BP的值是定值，值为10．
练习册系列答案
相关题目
【题目】观察表格：
|
|
| |
1条直线 0个交点 平面分成（1+1）块 | 2条直线 1个交点 平面分成（1+1+2）块 | 3条直线 （1+2）个交点 平面分成（1+1+2+3）块 | 4条直线 （1+2+3）个交点 平面分成（1+1+2+3+4）块 |
根据表格中的规律解答问题：
（1）5条直线两两相交，有 个交点，平面被分成 块；
（2）n条直线两两相交，有 个交点，平面被分成 块；
（3）应用发现的规律解决问题：一张圆饼切10刀（不许重叠），最多可得到 块饼．
