��Ŀ����
����Ŀ�����壺��һ��Խ���ȶ���һ��ԽDz���ȵ��ı��ν������ȶԽ��ı��Ρ���
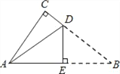
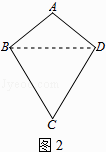
��1����֪����ͼ1���ı���ABCD�ǡ��ȶԽ��ı��Ρ�����A�١�C����A=70�㣬��B=80�㣮���C����D�Ķ�����
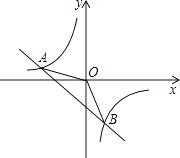
��2����̽�����ȶԽ��ı��Ρ�����ʱ����ͬѧ����һ�����ȶԽ��ı��Ρ�ABCD����ͼ2�������С�ABC=��ADC��AB=AD����ʱ������CB=CD����������֤���˽��ۣ�
��3����֪���ڡ��ȶԽ��ı��Ρ�ABCD�У���DAB=45�㣬��ABC=90�㣬AB=5��AD=4 ![]() ����Խ���AC�ij�Ϊ ��
����Խ���AC�ij�Ϊ ��
���𰸡�
��1��
�⣺���ı���ABCD�ǡ��ȶԽ��ı��Ρ�����A�١�C��
���D=��B=80�㣬
���C=360�㩁��A����B����D=360�㩁70�㩁80�㩁80��=130�㣻
��2��
֤������ͼ2��ʾ������BD��
��AB=AD��
���ABD=��ADB��
�ߡ�ABC=��ADC��
���ABC����ABD=��ADC����ADB��
���CBD=��CDB��
��CB=CD��
��3��![]()
����������3���⣺�����������
�ٵ���ADC=��ABC=90��ʱ���ӳ�AD��BC�ཻ�ڵ�E����ͼ3��ʾ��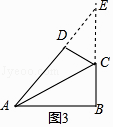
�ߡ�ABC=90�㣬��DAB=45�㣬AB=5�����E=45�㣬
��AE= ![]() AB=5
AB=5 ![]() ��
��
��DE=AE��AD=5 ![]() ��4
��4 ![]() �T
�T ![]() ��
��
�ߡ�EDC=90�㣬��E=45�㣬
��CD= ![]() ��
��
��AC= ![]() =
= ![]() =
= ![]() ��
��
�ڵ���BCD=��DAB=45��ʱ��
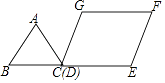
����D��DM��AB�ڵ�M��DN��BC�ڵ�N����ͼ4��ʾ��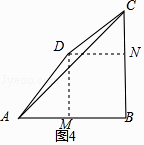
���AMD=90�㣬�ı���BNDM�Ǿ��Σ�
�ߡ�DAB=45�㣬
���ADM=45�㣬
��AM=DM= ![]() AD=4��
AD=4��
��BM=AB��AM=5��4=1��
���ı���BNDM�Ǿ��Σ�
��DN=BM=1��BN=DM=4��
�ߡ�BCD=45�㣬
��CN=DN=1��
��BC=CN+BN=5��
��AC= ![]() =5
=5 ![]() ��
��
�ʴ���������ڣ�
����������AC�ij�Ϊ ![]() ��
��
���Դ��ǣ� ![]() ��
��
��1�������ı���ABCD�ǡ��ȶԽ��ı��Ρ��ó���D=��B=80�㣬���ݶ�����ڽǺͶ��������C���ɣ���2������BD����AB=AD���ó���ABD=��ADB��֤����CBD=��CDB�����ɵó�CB=CD����3��������������ٵ���ADC=��ABC=90��ʱ���ӳ�AD��BC�ཻ�ڵ�E�����õ���ֱ�������ε��������AE���ó�DE���������Ǻ������CD���ɹ��ɶ������AC���ڵ���BCD=��DAB=45��ʱ������D��DM��AB�ڵ�M��DN��BC�ڵ�N�����AMD=90�㣬�ı���BNDM�Ǿ��Σ������AM��DM�����ɾ��ε����ʵó�DN=BM=1��BN=DM=4�����CN��BC�����ݹ��ɶ������AC���ɣ�
�����㾫����ͨ��������õ���ֱ�������κ��ɶ����ĸ�����յ���ֱ��������������ֱ�DZ���ȵ�ֱ�������Σ�����ֱ�������ε�����������ҵ���45�㣻ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2�����Խ����⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�