Question

【题目】将长为、宽为的长方形白纸按如图所示的方法黏合在一起，黏合部分的白纸宽为．

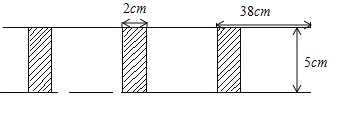
（1）求张白纸黏合的长度；

（2）设张白纸黏合后的总长为，写出与的函数关系式；（标明自变量的取值范围）

（3）用这些白纸黏合的长度能否为，并说明理由．

Answer 1

【答案】（1）张白纸黏合的长度为；（2）（x≥1，且x为整数）；（3）能，理由见解析．

【解析】

（1）5张白纸黏合，需黏合4次，重叠2×4=8cm，所以总长就可得到；
（2）x张白纸黏合，需黏合（x-1）次，重叠2（x-1）cm，所以总长可以表示出来；
（3）解当y=362时得到的方程，若x为自变量取值范围内的值则能，反之则不能．

（1）；

答：张白纸黏合的长度为；

（2）（x≥1，且x为整数）；

（3）能，当y=362时，得到：36x+2=362，解得x=10．