题目内容
【题目】已知![]() 和
和![]() 为等腰三角形,
为等腰三角形,![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,点
上,点![]() 在射线
在射线![]() 上.
上.

(1)如图1,若∠BAC=60°,点F与点C重合,求证:AF=AE+AD;
(2)如图2,若AD=AB,求证:AF=AE+BC. .
【答案】(1)见解析;(2)见解析;
【解析】
(1)由∠BAC=∠EDF=60°,推出△ABC、△DEF为等边三角形,于是得到∠BCE+∠ACE=∠DCA+∠ECA=60°,推出△BCE≌△ACD(SAS),根据全等三角形的性质得到AD=BE,即可得到结论;
(2)在FA上截取FM=AE,连接DM,推出△AED≌△MFD(SAS),根据全等三角形的性质得到DA=DM=AB=AC,∠ADE=∠MDF,证得∠ADM=∠EDF=∠BAC,推出△ABC≌△DAM(SAS),根据全等三角形的性质得到AM=BC,即可得到结论.
证明:(1)∵∠BAC=∠EDF=60°,
∴△ABC、△DEF为等边三角形,
∴∠BCE+∠ACE=∠DCA+∠ECA=60°,
在△BCE和△ACD中
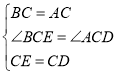
∴△BCE≌△ACD(SAS),
∴AD=BE,
∴AE+AD=AE+BE=AB=AF;
(2)在FA上截取FM=AE,连接DM,
∵∠BAC=∠EDF,
∴∠AED=∠MFD,
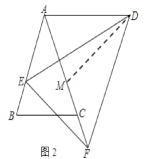
在△AED和△MFD中
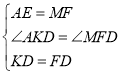 ,
,
∴△AED≌△MFD(SAS),
∴DA=DM=AB=AC,∠ADE=∠MDF,
∴∠ADE+∠EDM=∠MDF+∠EDM,
即∠ADM=∠EDF=∠BAC,
在△ABC和△DAM中,
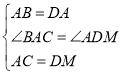 ,
,
∴△ABC≌△DAM(SAS),
∴AM=BC,
∴AE+BC=FM+AM=AF.
即AF=AE+BC.

【题目】李老师为了了解学生暑期在家的阅读情况,随机调查了20名学生某一天的阅读小时数,具体情况统计如下:
阅读时间 (小时) | 2 | 2.5 | 3 | 3.5 | 4 |
学生人数(名) | 1 | 2 | 8 | 6 | 3 |
则关于这20名学生阅读小时数的说法正确的是( )
A. 众数是8 B. 中位数是3 C. 平均数是3 D. 方差是0.34






