题目内容
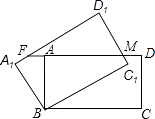
【题目】如图四边形ABCD中,AD∥BC,∠BCD=90°,∠BAD的平分线AG交BC于点G.
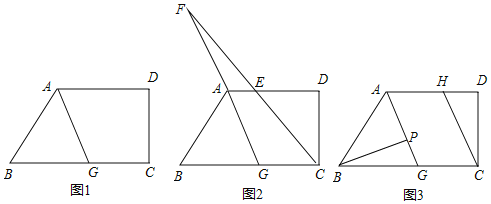
(1)求证:∠BAG=∠BGA;
(2)如图2,∠BCD的平分线CE交AD于点E,与射线GA相交于点F,∠B=50°.
①若点E在线段AD上,求∠AFC的度数;
②若点E在DA的延长线上,直接写出∠AFC的度数;
(3)如图3,点P在线段AG上,∠ABP=2∠PBG,CH∥AG,在直线AG上取一点M,使∠PBM=∠DCH,请直接写出∠ABM:∠PBM的值.
【答案】(1)证明见解析;(2)①20°;②160°;(3)![]() 或
或![]()
【解析】
(1)根据AD//BC可知∠GAD=∠BGA,由AG平分∠BAD可知∠BAG=∠GAD,即可得答案.(2)①根据CF平分∠BCD,∠BCD=90°,可求出∠GCF的度数,由AD//BC可求出∠AEF和∠DAB的度数,根据三角形外角的性质求出∠AFC的度数即可;②根据三角形外角性质求出即可;(3)根据M点在BP的上面和下面两种情况讨论,分别求出∠PBM和∠ABM的值即可.
(1)∵AD∥BC,
∴∠GAD=∠BGA,
∵AG平分∠BAD,
∴∠BAG=∠GAD,
∴∠BAG=∠BGA;
(2)①∵CF平分∠BCD,∠BCD=90°,
∴∠GCF=45°,
∵AD∥BC,∠ABC=50°,
∴∠AEF=∠GCF=45°;∠DAB=180°﹣50°=130°,
∵AG平分∠BAD,
∴∠BAG=∠GAD=65°,
∴∠AFC=65°﹣45°=20°;
②如图:
∵∠AGB=65°,∠BCF=45°,
∴∠AFC=∠CGF+∠BCF=115°+45°=160°;
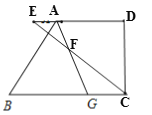
(3)有两种情况:
①当M在BC的下方时,如图:∵∠ABC=50°,∠ABP=2∠PBG,
∴∠ABP=(![]() )°,∠PBG=(
)°,∠PBG=(![]() )°,
)°,
∵AG∥CH,
∴∠BCH=∠AGB=65°,∵∠BCD=90°,∴∠DCH=∠PBM=90°﹣65°=25°,
∴∠ABM=∠ABP+∠PBM=(![]() +25)°=(
+25)°=(![]() )°,
)°,
∴∠ABM:∠PBM=(![]() )°:25°=
)°:25°=![]() ;
;
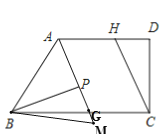
②当M在BC的上方时,如图:
同理得:∠ABM=∠ABP﹣∠PBM=(![]() ﹣25)°=(
﹣25)°=(![]() )°,
)°,
∴∠ABM:∠PBM=(![]() )°:25°=
)°:25°=![]() ;
;
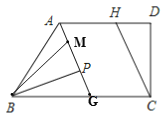
综上,∠ABM:∠PBM的值是![]() 或
或![]() .
.