题目内容
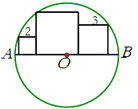
【题目】如图，AB是
的直径，紧挨着的三个正方形依次排列在直径AB上，且各有一个顶点在
上，若两侧两个正方形边长分别为2和3，则中间正方形的边长为_____________________．
【答案】
【解析】连接AO、PO、EO，设O的半径为r，OC=x，OG=y，
由勾股定理可知：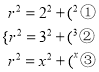 
③②得到： 
，
∴
，
∴
，
∵x+y+3≠0，
∴x+y3=y+3x，
∴x=3,代入①得到r=29,代入③得到：29=9+(x+y) ，
∴(x+y) =20，
∵x+y>0，
∴x+y=
，
点睛: 通过直角三角形和圆的半径建立三个正方形的边长关系，列出关系式，通过等式关系消除多余的未知数最后获得所求未知数x和y的方程,通过计算，并利用x+y>0的条件求出x+y的值.
练习册系列答案
新非凡教辅冲刺100分系列答案
相关题目
【题目】为了加强公民的节水意识，合理利用水资源，某市采用价格调控的手段达到节水的目的，该市自来水收费的收费标准如下表：
收费标准（注：水费按月份结算） | |
每月用水量 | 单价（元/立方米） |
不超出 |
|
超出 |
|
超出 |
|
例如：某户居民
月份用水
立方米，应收水费为
（元）．
请根据上表的内容解答下列问题：
（
）若某户居民
月份用水
立方米，则应收水费多少元？
（
）若某户居民
月份用水
立方米（其中
），请用含
的代数式表示应收水费．
（
）若某户居民
、
两个月共用水
立方米（
月份用水量超过了
立方米），设
月份用水
立方米，请用含
的代数式表示该居民
、
两个月共交水费多少元．
