题目内容
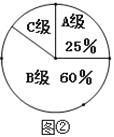
【题目】下面是小明同学设计的“过圆外一点作圆的切线”的尺规作图的过程.
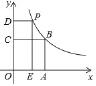
已知:如图1,![]() 和
和![]() 外的一点
外的一点![]() 求作:过点P作
求作:过点P作![]() 的切线.
的切线.
作法:如图2,
![]() 连接OP;
连接OP;
![]() 作线段OP的垂直平分线MN,直线MN交OP于C;
作线段OP的垂直平分线MN,直线MN交OP于C;
![]() 以点C为圆心,CO为半径作圆,交
以点C为圆心,CO为半径作圆,交![]() 于点A和B;
于点A和B;
![]() 作直线PA和
作直线PA和![]() 则PA,PB就是所求作的
则PA,PB就是所求作的![]() 的切线.
的切线.
根据上述作图过程,回答问题:
![]() 用直尺和圆规,补全图2中的图形;
用直尺和圆规,补全图2中的图形;
![]() 完成下面的证明:证明:连接OA,OB,
完成下面的证明:证明:连接OA,OB,
![]() 由作图可知OP是
由作图可知OP是![]() 的直径,
的直径,
![]() ,
,
![]() ,
,![]() ,图2
,图2
又![]() 和OB是
和OB是![]() 的半径,
的半径,
![]() ,PB就是
,PB就是![]() 的切线
的切线![]() ______
______![]() 填依据
填依据![]() .
.
【答案】(1)见解析;(2)证明见解析.
【解析】
(1)用圆规和直尺根据作图步骤补齐图形即可;
(2)根据圆周角定理及切线的判定方法证明即可.
解:(1)如图,PA、PB为所作;
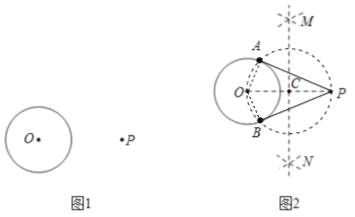
(2)证明:连接OA,OB,
∵由作图可知OP是⊙C的直径,
∴∠OAP=∠OBP=90°,
∴OA⊥PA,OB⊥PB,图2
又∵OA和OB是⊙O的半径,
∴PA,PB就是⊙O的切线(过半径的外端且与半径垂直的直线为圆的切线).
故答案为:过半径的外端且垂直于该半径的直线为圆的切线.

练习册系列答案
相关题目
【题目】盒中有若干枚黑棋和白棋,这些棋除颜色外无其他差别,现让学生进行摸棋试验:每次摸出一枚棋,记录颜色后放回摇匀.重复进行这样的试验得到以下数据:
摸棋的次数n | 100 | 200 | 300 | 500 | 800 | 1000 |
摸到黑棋的次数m | 24 | 51 | 76 | 124 | 201 | 250 |
摸到黑棋的频率 | 0.240 | 0.255 | 0.253 | 0.248 | 0.251 | 0.250 |
(1)根据表中数据估计从盒中摸出一枚棋是黑棋的概率是 ;(精确到0.01)
(2)若盒中黑棋与白棋共有4枚,某同学一次摸出两枚棋,请计算这两枚棋颜色不同的概率,并说明理由