题目内容
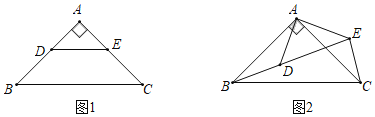
【题目】把两个等腰直角△ABC和△ADE按如图1所示的位置摆放,将△ADE绕点A按逆时针方向旋转,如图2,连接BD,EC,设旋转角为α(0°<α<360°)
(1)当DE⊥AC时,AD与BC的位置关系是 ,AE与BC的位置关系是 ;
(2)如图2,当点D在线段BE上时,求∠BEC的度数;
(3)当旋转角α= 时,△ABD的面积最大.
【答案】(1)垂直,平行;(2)∠BEC=90°;(3)90°或270°
【解析】
(1)根据题意画出图形,利用三线合一性质可证明AD与BC垂直,再根据平行线的判定可证明AE与BC平行;
(2)利用等腰三角形的性质证明△BAD≌△CAE,求出∠ADB=∠AEC=135°,所以∠BEC=∠AEC﹣45°=90°;
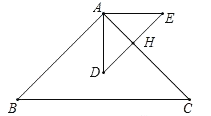
(3)根据题意画出图形,由题意知,点D的轨迹在以A为圆心,AD为半径的圆上,在△ABD中,当以AB为底时,当点D到AB的距离最大时,△ABD的面积最大,当AD⊥AB时,△ABD的面积最大,所以旋转角为90°或270°.
解:(1)设AC与DE交于点H,
在等腰直角△ABC和△ADE中,
∠BAC=∠DAE=90°,AD=AE,AB=AC,∠B=∠C=45°,
∵DE⊥AC,
∴∠DAH=∠EAH=![]() ∠DAE=45°,
∠DAE=45°,
∴∠BAD=∠BAC﹣∠DAH=45°,
∴∠BAD=∠DAH,
∴AD⊥BC,
∵∠EAH=∠C=45°,
∴AE∥BC,
故答案为:垂直,平行;
(2)在等腰直角△ADE中,AD=AE,∠DAE=90°,
在等腰直角△ABC中,AB=AC,∠BAC=90°,
∵∠BAD=∠BAC﹣∠DAC=90°﹣∠DAC,
∠CAE=∠DAE﹣∠DAC=90°﹣∠DAC,
∴∠BAD=∠CAE,
又∵AB=AC,AD=AE,
∴△BAD≌△CAE(SAS),
∴∠ADB=∠AEC=180﹣∠ADE=135°,
∴∠BEC=∠AEC﹣45°=135﹣45°=90°;
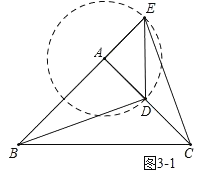
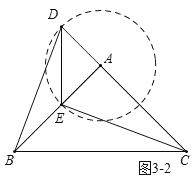
(3)由题意知,点D的轨迹在以A为圆心,AD为半径的圆上,如图3﹣1,3﹣2,
在△ABD中,当以AB为底时,当点D到AB的距离最大时,△ABD的面积最大,
故如图3﹣1,3﹣2所示,当AD⊥AB时,△ABD的面积最大,所以旋转角为90°或270°,
故答案为90°或270°.

 中考解读考点精练系列答案
中考解读考点精练系列答案