题目内容
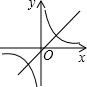
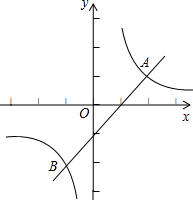
如图，Rt△ABC的直角边BC在x轴正半轴上，斜边AC边上的中线BD反向延长线交y轴负半轴于E，双曲线y=
(x＞0)的图象经过点A，若S△BEC=8，则k等于（ ）
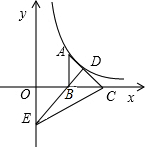
| k |
| x |
| A．8 | B．16 | C．24 | D．28 |
∵BD为Rt△ABC的斜边AC上的中线，
∴BD=DC，∠DBC=∠ACB，
又∠DBC=∠EBO，∴∠EBO=∠ACB，
又∠BOE=∠CBA=90°，
∴△BOE∽△CBA，
∴
=
，即BC×OE=BO×AB．
又∵S△BEC=8，即BC×OE=2×8=16=BO×AB=|k|．
又由于反比例函数图象在第一象限，k＞0．
所以k等于16．
故选B．
∴BD=DC，∠DBC=∠ACB，
又∠DBC=∠EBO，∴∠EBO=∠ACB，
又∠BOE=∠CBA=90°，
∴△BOE∽△CBA，
∴
| BO |
| BC |
| OE |
| AB |
又∵S△BEC=8，即BC×OE=2×8=16=BO×AB=|k|．
又由于反比例函数图象在第一象限，k＞0．
所以k等于16．
故选B．
练习册系列答案
阅读快车系列答案
相关题目
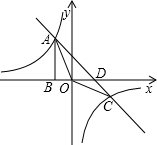
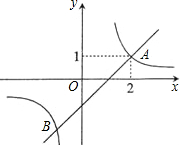
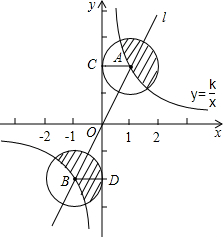点A（1，2），点B（m，-2）．分别过A、B作AC⊥y轴于C，BD⊥y轴于D，再以AC、BD为半径作⊙A和⊙B．
