题目内容
【题目】如图,是用棋子摆成的图案,摆第1个图案需要7枚棋子,摆第2个图案需要19枚棋子,摆第3个图案需要37枚棋子,按照这样的方式摆下去,则摆第6个图案需要 枚棋子,摆第n个图案需要 枚棋子.

【答案】127,3n2+3n+1(n∈N+)
【解析】方法一:
解:∵n=1时,总数是6+1=7;
n=2时,总数为6×(1+2)+1=19;
n=3时,总数为6×(1+2+3)+1=37枚;
…;
∴n=6时,总数为6×(1+2+3…+6)+1=127枚;
…;
∴n=n时,有6×(1+2+3+…n)+1=6×![]() +1=3n2+3n+1枚.
+1=3n2+3n+1枚.
故答案为:127,3n2+3n+1(n∈N+).
方法二:
n=1,s=7;n=2,s=19;n=3,s=37,
经观察.此数列为二阶等差(即后项减前项,两次作差,差相等)
设:s=an2+bn+c,
∴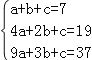 ,
,
∴![]() ,
,
∴s=3n2+3n+1,把n=6代入,s=127.
方法三:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴a6=37+24+30+36=127.

练习册系列答案
相关题目