题目内容
【题目】准备一张矩形纸片,按如图操作:将△ABE沿BE翻折,使点A落在对角线BD上的M点,将△CDF沿DF翻折,使点C落在对角线BD上的N点.

(1)、求证:四边形BFDE是平行四边形;
(2)、若四边形BFDE是菱形, AB=2,求菱形BFDE的面积.
【答案】(1)、证明过程见解析;(2)、![]()
【解析】
试题分析:(1)、根据矩形的性质可得∠ABD=∠CDB,根据折叠可得∠EBD=∠FDB,则BE∥DF,根据两组对边分别平行的四边形为平行四边形进行证明;(2)、根据菱形可得BE=DE,有折叠可得BM=AB=2,则DM=BM=2,BD=4,根据勾股定理可得AD=2![]() ,设DE=x,则AE=2
,设DE=x,则AE=2![]() -x,BE=x,根据Rt△ABE的勾股定理得出x的值,然后计算菱形的面积.
-x,BE=x,根据Rt△ABE的勾股定理得出x的值,然后计算菱形的面积.
试题解析:(1)、∵四边形ABCD是矩形
∴AB∥CD,AD∥BC
∴∠ABD=∠CDB
由折叠知:∠EBD=∠ABD,∠FDB=∠CDB
∴∠EBD=∠FDB
∴BE//DF
∴四边形BFDE是平行四边形;
(2)、∵四边形BFDE是菱形
∴ BE=DE
由折叠知:∠EMB=∠A=90°BM=AB=2
∴DM=BM=2
∴BD=4
由勾股定理解得AD=2![]()
设DE=x,则AE=2![]() ―x,BE=x
―x,BE=x
在Rt△ABE中,AE2+AB2=BE2
(2![]() ―x)2+22=x2
―x)2+22=x2
解得:x=![]()
∴菱形BFDE的面积为![]() ×2=
×2=![]()

 教学练新同步练习系列答案
教学练新同步练习系列答案【题目】随着车辆的增加,交通违规的现象越来越严重,交警对某雷达测速区检测到的一组汽车的时速数据进行整理,得到其频数及频率如表(未完成):
时速数据段 | 频数 | 频率 |
30﹣40 | 10 | 0.05 |
40﹣50 | 36 | ___ |
50﹣60 | ___ | 0.39 |
60﹣70 | ___ | ___ |
70﹣80 | 20 | 0.10 |
总计 | 200 | 1 |
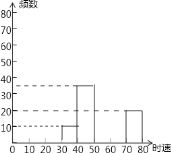
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果汽车时速超过60千米即为违章,则这次检测到的违章车辆共有 辆.
