题目内容
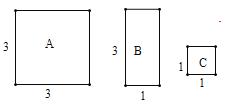
【题目】如图，有A、B、C三种不同型号的卡片，每种卡片各有9张.其中A型卡片是边长为3的正方形，B型卡片是相邻两边长分别为3、1的长方形，C型卡片是边长为1的正方形.从其中取若干张卡片（每种卡片至少取1张），若把取出的这些卡片拼成一个正方形，则所拼正方形的边长的最大值是______.
【答案】10
【解析】
根据题意每种卡片各有9张，每种至少取1张，拼成的正方形的边长要最大，则每种卡片应尽量多取，而全部用完时三种卡片的面积和为117，则边长不是整数无法拼成．那么只需要面积比117小，又是平方数即可，所以最大面积为100，边长为10．
A型卡片的面积为9，B型卡片的面积为3，C型卡片的面积为1，
∵拼成的正方形的边长要最大，
∴拼成的正方形面积要最大，
∵9×9+9×3+9×1=117
∴当拼成的正方形面积为100时最大，则边长为10，
此时：A型9张，B型6张，C型1张，
A型9张，B型5张，C型4张，
A型9张，B型4张，C型7张，
故答案为：10．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
【题目】足球运动员将足球沿与地面成一定角度的方向踢出，足球飞行的路线是一条抛物线，不考虑空气阻力，足球距离地面的高度h（单位：m）与足球被踢出后经过的时间t（单位：s）之间的关系如下表：
t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
h | 0 | 8 | 14 | 18 | 20 | 20 | 18 | 14 | … |
下列结论：①足球距离地面的最大高度为20m；②足球飞行路线的对称轴是直线t= 
；③足球被踢出9s时落地；④足球被踢出1.5s时，距离地面的高度是11m．其中正确结论的个数是（ ）
A.1
B.2
C.3
D.4
