题目内容
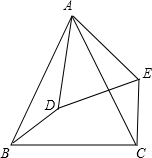 如图,已知△ABC与△ADE都是等腰三角形,且它们的顶角∠BAC=∠DAE.
如图,已知△ABC与△ADE都是等腰三角形,且它们的顶角∠BAC=∠DAE.求证:BD=CE.
分析:根据等腰三角形的性质可得AB=AC,AD=AE,∠BAC=∠DAE,再结合图形根据角的和差可得∠BAD=∠CAE,从而运用SAS可证明△ABD≌△ACE,所以BD=CE.
解答:证明:∵△ABC为等腰三角形,
∴AB=AC,
同理AD=AE.
∵∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE.
在△ABD与△ACE中,
,
∴△ABD≌△ACE,
∴BD=CE.
∴AB=AC,
同理AD=AE.
∵∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE.
在△ABD与△ACE中,
|
∴△ABD≌△ACE,
∴BD=CE.
点评:本题主要考查了全等三角形的判定与性质及等腰三角形的性质,注意熟记全等三角形的判定方法和性质.

练习册系列答案
相关题目
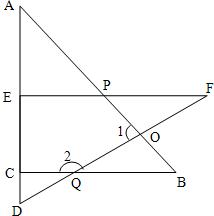 23、如图:已知△ABC与△DEF是一副三角板的拼图,A,E,C,D在同一条线上.
23、如图:已知△ABC与△DEF是一副三角板的拼图,A,E,C,D在同一条线上.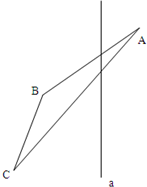 21、如图,已知△ABC与直线a、作出△ABC关于a的对称三角形△A′B′C′.(不写作法,保留作图痕迹)
21、如图,已知△ABC与直线a、作出△ABC关于a的对称三角形△A′B′C′.(不写作法,保留作图痕迹)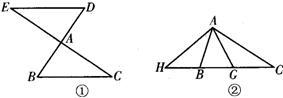
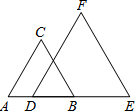 (2012•河东区一模)如图,已知△ABC与△DEF均为等边三角形,则图中的相似三角形有
(2012•河东区一模)如图,已知△ABC与△DEF均为等边三角形,则图中的相似三角形有