题目内容
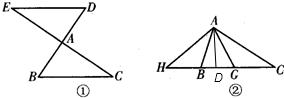
24、如图①，已知△ABC与△ADE关于点A成中心对称，∠B=50°，△ABC的面积为24，BC边上的高为5，若将△ADE向下折叠，如图②点D落在BC的G点处，点E落在CB的延长线的H点处，且BH=4，则∠BAG=
80
度，△ABG的面积是14
．分析：根据中心对称的性质和折叠的性质计算即可，同时运用了三角形的面积公式．
解答：解：依题意有AD=AB=AG，AE=AH=AC．
又∠B=50°，则∠BAG=180°-50°×2=80°；
作AD⊥BC于D，根据三角形的面积公式得到BC=9.6．
根据等腰三角形的三线合一，
可以证明CG=BH=4，则BG=5.6．
根据三角形的面积公式得△ABG的面积是14．
又∠B=50°，则∠BAG=180°-50°×2=80°；
作AD⊥BC于D，根据三角形的面积公式得到BC=9.6．
根据等腰三角形的三线合一，
可以证明CG=BH=4，则BG=5.6．
根据三角形的面积公式得△ABG的面积是14．
点评：此题能够根据中心对称的性质和折叠的性质发现相等的线段，解题的关键是熟练运用等腰三角形的三线合一的性质进行证明HB=CG．
练习册系列答案
相关题目
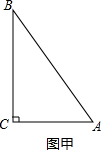定义：若某个图形可分割为若干个都与他相似的图形，则称这个图形是自相似图形．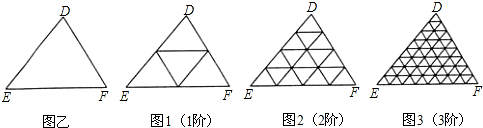
如图，若已知△ABC中，D、E分别为AB、AC的中点，则可得DE∥BC，且DE=
