��Ŀ����
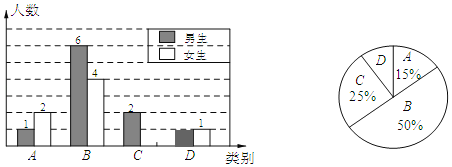
����Ŀ������ʦΪ�˽�ijУѧ�������ѧ��ǰԤϰ�ľ���������Բ���ѧ�������˸��ٵ��飬������������Ϊ���࣬A���ܺã�B���Ϻã�C��һ�㣻D���ϲ���Ƴ�����ͳ��ͼ��
��1������ʦһ�������˶�����ͬѧ��������������ͳ��ͼ����������
��2������У��1000��ѧ��������ѧ��ǰԤϰ���ܺá��͡��Ϻá��ܹ�Լ�����ˣ�
��3��Ϊ�˹�ͬ����������ʦ��ӱ������A���D��ѧ���и����ѡȡһλͬѧ���С�һ��һ������ѧϰ�������ѡ��λͬѧǡ����һλ��ͬѧ��һλŮͬѧ�ĸ��ʣ���Ҫ���б�����״ͼ��
���𰸡���1��20��ͼ�����������2��650����3��![]()
��������
��1������A��ѧ����������A��ѧ����ռ�ٷֱȿɵõ���ѧ���������õ����ѧ����������C����ռ�İٷֱȣ��ټ�ȥC������������Ӷ����C���Ů�������õ����ѧ��������ȥA��B��C���ѧ������D���Ů�������Ӷ����D��������������ɲ�ȫͳ��ͼ��
��2������������������˼�����ɵã�
��3�����������Ȼ�����״ͼ���ٸ��ݸ��ʹ�ʽ���ɵó��𰸣�
��1������������Ϊ3��15%��20��C����Ů���У�20��25%��2��3��������
D����������20��3��10��5��1��1���ˣ���
����ͳ��ͼ����������ͼ��ʾ��
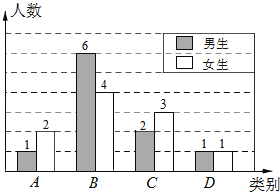
��2��1000��65%��650�ˣ�
����ѧ��ǰԤϰ���ܺ��������Ϻ����ܹ�Լ650�ˣ�
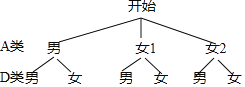
��3���������⻭ͼ���£�
 ��
��
����״ͼ�ɵù���6�ֿ��ܵĽ��������ǡ��һ����ͬѧ��һ��Ůͬѧ�Ľ����3�У�
����ǡ����һ����ͬѧ��һ��Ůͬѧ�ĸ�����![]() ��
��

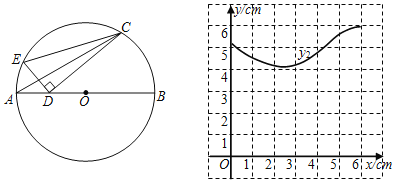
����Ŀ����ͼ��AB��ԲO��ֱ������C��ԲO��һ�㣬��CAB��30�㣬D��ֱ��AB��һ���㣬����CD������D��CD�Ĵ��ߣ���ԲO������һ�������Ϊ��E����Eλ��ֱ��CD�Ϸ�����ࣩ������EC����֪AB��6cm����A��D�����ľ���Ϊxcm��C��D�����ľ���Ϊy1cm��E��C�����ľ���Ϊy2cm��Сѩ����ѧϰ�����ľ��飬�ֱ�Ժ���y1��y2���Ա���x�ı仯���仯�Ĺ��ɽ�����̽����������Сѩ��̽�����̣�
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 5.2 | 4.4 | 3.6 | 3.0 | 2.7 | 2.7 | �� �� |
y2/cm | 5.2 | 4.6 | 4.2 | �� �� | 4.8 | 5.6 | 6.0 |
��1�������±����Ա���x��ֵ����ȡ�㡢��ͼ���������ֱ�õ���y1��y2��x�ļ����Ӧֵ���뽫����������������һλС����
��2����ͬһƽ��ֱ������ϵxOy�У�y2��ͼ����ͼ��ʾ�������ȫ��ı��и�����ֵ����Ӧ�ĵ㣨x��y1������x��y2��������������y1��ͼ��
��3����Ϻ���ͼ������⣺����ECD��60��ʱ��AD�ij���ԼΪ�� ��cm��