题目内容
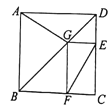
【题目】如图,四边形ABCD为矩形,过点D作对角线BD的垂线,交BC的延长线于点E,取BE的中点F,连接DF,DF=4.设AB=x,AD=y,则x2+(y﹣4)2的值为 .

【答案】16
【解析】
试题分析:根据矩形的性质得到CD=AB=x,BC=AD=y,然后利用直角△BDE的斜边上的中线等于斜边的一半得到:BF=DF=EF=4,则在直角△DCF中,利用勾股定理求得
x2+(y﹣4)2=DF2.
解:∵四边形ABCD是矩形,AB=x,AD=y,
∴CD=AB=x,BC=AD=y,∠BCD=90°.
又∵BD⊥DE,点F是BE的中点,DF=4,
∴BF=DF=EF=4.
∴CF=4﹣BC=4﹣y.
∴在直角△DCF中,DC2+CF2=DF2,即x2+(4﹣y)2=42=16,
∴x2+(y﹣4)2=x2+(4﹣y)2=16.
故答案是:16.

练习册系列答案
相关题目
【题目】甲、乙、丙三位运动员在相同条件下各射靶10次,每次射靶的成绩如下:
甲:9,10,8,5,7,8,10,8,8,7;
乙:5,7,8,7,8,9,7,9,10,10;
丙:7,6,8,5,4,7,6,3,9,5.
(1)根据以上数据完成下表:
平均数 | 中位数 | 方差 | |
甲 | 8 | 8 | |
乙 | 8 | 8 | 2.2 |
丙 | 6 | 3 |
(2)依据表中数据分析,哪位运动员的成绩最稳定,并简要说明理由.