题目内容
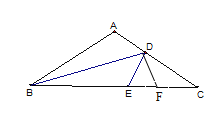
【题目】如图，在△ABC中，AB=AC，∠A=100°，沿BD对折恰使点A落在BC边上的E点，EC上有一点F，且DF=CF，（1）求证:DF=AD，(2) 猜想：BC与BD+AD的关系，并说明理由。
【答案】详见解析.
【解析】试题分析：由折叠的性质可得AD=DE，∠DEB=∠A=100°；由AB=AC，∠A=100°得，∠C=80°，再由DF=CF得∠DFE=80°，从而可得DE=DF，进而证得结论；
（2）由折叠易证∠DBF=20°，由（1）可解得∠BDF=80°，从而证得BD=BF，由（1）可知AD=DE=DF=FC，从而得证.
试题解析：(1) ∵∠A=100°，AB=AC，∴∠C=40°，
又DF=CF，∴∠DFE=80°，
∵∠BED=∠A=100°，∴∠DEF=80°，
∴DE=DF，∵DE=AD，∴DF=AD.
(2)BC=BD+AD，
∵∠DEF=∠DFE=80°，∴∠EDF=20°，∴∠BDF=80°，
∴BD=BF，∵CF=DF=AD，
∴BC=BF+FC=BD+AD.
练习册系列答案
相关题目
