题目内容
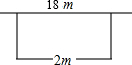
如图,长方形鸡场的一边靠墙(墙长18m),墙对面有一个2m宽的门,另三边用竹篱笆围成,篱笆总长33m,
(1)若鸡场面积为150m2,求鸡场的长和宽各为多少m?
(2)求围成的鸡场的最大面积.
(1)若鸡场面积为150m2,求鸡场的长和宽各为多少m?
(2)求围成的鸡场的最大面积.

(1)设鸡场的长为x m,①若靠墙的一边为长则宽为:
m,由题意得:
x×
=150,
即:x2-35x+300=0,
解得:x1=15,x2=20
由于x=20m>18m,不合题意舍去:
所以此时鸡场的长为15m,宽为:
=10m.
②若靠墙一边为宽,则宽为:33+2-2x=35-2xm,由题意得:
x(35-2x)=150,
即:2x2-35x+150=0,
解得:x1=10m,x2=7.5m,
当x=10m时,宽为:35-2x=15m>10m,不合题意舍去;
当x=7.5m时,宽为:35-2x=20m>18m>5m,不合题意舍去;
所以靠墙的一边应当为长,它的相邻边为宽,
即:若鸡场的面积为150cm2时,鸡场的长和宽各为15m、10m.
(2)若靠墙一边为长时,鸡场的面积=x(
)=-
(x-
)2+
,
此时鸡场的最大面积为:
cm2;
若靠墙一边为宽时,鸡场的面积为=x(35-2x)=-2(x-
)2+
,
此时鸡场的最大面积为:
cm2,
所以要求的鸡场的最大面积为:
cm2.
| 33-x+2 |
| 2 |
x×
| 33-x+2 |
| 2 |
即:x2-35x+300=0,
解得:x1=15,x2=20
由于x=20m>18m,不合题意舍去:
所以此时鸡场的长为15m,宽为:
| 33-15+2 |
| 2 |
②若靠墙一边为宽,则宽为:33+2-2x=35-2xm,由题意得:
x(35-2x)=150,
即:2x2-35x+150=0,
解得:x1=10m,x2=7.5m,
当x=10m时,宽为:35-2x=15m>10m,不合题意舍去;
当x=7.5m时,宽为:35-2x=20m>18m>5m,不合题意舍去;
所以靠墙的一边应当为长,它的相邻边为宽,
即:若鸡场的面积为150cm2时,鸡场的长和宽各为15m、10m.
(2)若靠墙一边为长时,鸡场的面积=x(
| 33-x+2 |
| 2 |
| 1 |
| 2 |
| 35 |
| 2 |
| 1225 |
| 8 |
此时鸡场的最大面积为:
| 1225 |
| 8 |
若靠墙一边为宽时,鸡场的面积为=x(35-2x)=-2(x-
| 35 |
| 4 |
| 1225 |
| 8 |
此时鸡场的最大面积为:
| 1225 |
| 8 |
所以要求的鸡场的最大面积为:
| 1225 |
| 8 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
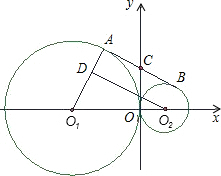
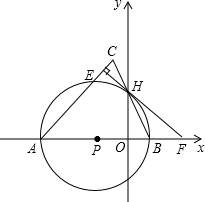 上,B点的坐标为(1,0).
上,B点的坐标为(1,0).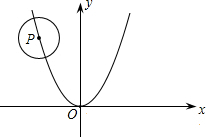
 角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由. 点C,B的横坐标,且此抛物线过点A(3,6).
点C,B的横坐标,且此抛物线过点A(3,6).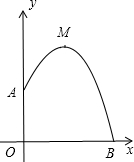 图)如果抛物线的最高点M离墙1米,离地面
图)如果抛物线的最高点M离墙1米,离地面