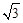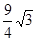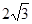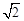题目内容
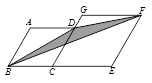
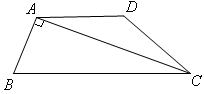
如图，四边形ABCD是梯形，AD∥BC，CA是∠BCD的平分线，且AB⊥AC，AB=4，AD="6" ，则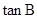
=
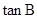=A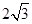． | B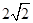． | C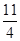． | D． |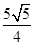
B。
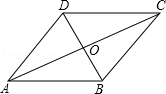
如图，过A作AE∥DC交BC于点E，连接DE，交AC于点O，则
∵AD∥BC，∴四边形AECD是平行四边形，∠DAC=∠ACB。
∵CA是∠BCD的平分线，∴∠DCA=∠ACB。∴∠DCA=∠DAC。
∴AD=CD。∴四边形AECD是菱形。∴AO=OC，DE⊥AC。
又∵AB⊥AC，∴OE∥AB。∴BE=EC。
∵AD=6，∴BC=2EC=2AD=12。
又∵AB=4，∴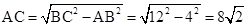
。
∴
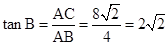。故选B。
∵AD∥BC，∴四边形AECD是平行四边形，∠DAC=∠ACB。
∵CA是∠BCD的平分线，∴∠DCA=∠ACB。∴∠DCA=∠DAC。
∴AD=CD。∴四边形AECD是菱形。∴AO=OC，DE⊥AC。
又∵AB⊥AC，∴OE∥AB。∴BE=EC。
∵AD=6，∴BC=2EC=2AD=12。
又∵AB=4，∴
。∴
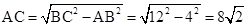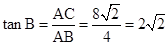。故选B。
练习册系列答案
阅读快车系列答案
相关题目
．
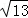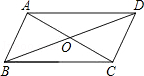
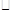ABCD的周长为l6cm，对角线AC与BD相交于点O，
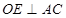交AD于E，连接CE，则△DCE的周长为( )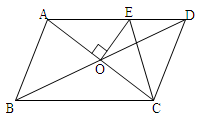
时，四边形BA，CD为等腰梯形；
