题目内容
定义{a,b,c}为函数y=ax2+bx+c的“特征数”.如:函数y=x2-2x+3的“特征数”是{1,-2,3},函数y=2x+3的“特征数”是{0,2,3},函数y=-x的“特征数”是{0,-1,0}(1)将“特征数”是{1,-4,1}的函数的图象向下平移2个单位,得到一个新函数图象,求这个新函数图象的解析式;
(2)“特征数”是
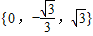 的函数图象与x、y轴分别交点C、D,“特征数”是
的函数图象与x、y轴分别交点C、D,“特征数”是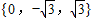 的函数图象与x轴交于点E,点O是原点,判断△ODC与△OED是否相似,请说明理由.
的函数图象与x轴交于点E,点O是原点,判断△ODC与△OED是否相似,请说明理由.
【答案】分析:(1)根据函数“特征数”写出函数的解析式,再根据平移后二次函数的变化情况写出函数图象向下平移2个单位的新函数的解析式.
(2)根据已知得出一次函数解析式,进而求出图象与坐标轴交点,再利用相似三角形的判定得出即可.
解答: 解:(1)∵函数y=x2-2x+3的“特征数”是{1,-2,3},函数y=2x+3的“特征数”是{0,2,3},函数y=-x的“特征数”是{0,-1,0},
解:(1)∵函数y=x2-2x+3的“特征数”是{1,-2,3},函数y=2x+3的“特征数”是{0,2,3},函数y=-x的“特征数”是{0,-1,0},
∴“特征数”是{1,-4,1}的函数解析式是:y=x2-4x+1=(x-2)2-3,
∵函数的图象向下平移2个单位,
∴y=(x-2)2-5=x2-4x-1,
(2)∵“特征数”是 的函数图象与x、y轴分别交点C、D,
的函数图象与x、y轴分别交点C、D,
∴函数解析式为:y= ,
,
∴图象与x、y轴分别点C(3,0)、D(0, ),
),
∵“特征数”是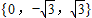 的函数图象与x轴交于点E,
的函数图象与x轴交于点E,
∴函数解析式为:y=
∴图象与x、y轴分别点E(1,0)、D(0,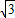 ),
),
∴OD=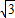 ,OC=3,OD=1.
,OC=3,OD=1.
∴OD2=OC×OE,
∴△ODC∽△OED.
点评:此题主要考查了二次函数的综合应用,结合“特征数”的定义考查一次函数,二次函数的综合应用,综合性强,能力要求高.
(2)根据已知得出一次函数解析式,进而求出图象与坐标轴交点,再利用相似三角形的判定得出即可.
解答:
 解:(1)∵函数y=x2-2x+3的“特征数”是{1,-2,3},函数y=2x+3的“特征数”是{0,2,3},函数y=-x的“特征数”是{0,-1,0},
解:(1)∵函数y=x2-2x+3的“特征数”是{1,-2,3},函数y=2x+3的“特征数”是{0,2,3},函数y=-x的“特征数”是{0,-1,0},∴“特征数”是{1,-4,1}的函数解析式是:y=x2-4x+1=(x-2)2-3,
∵函数的图象向下平移2个单位,
∴y=(x-2)2-5=x2-4x-1,
(2)∵“特征数”是
 的函数图象与x、y轴分别交点C、D,
的函数图象与x、y轴分别交点C、D,∴函数解析式为:y=
 ,
,∴图象与x、y轴分别点C(3,0)、D(0,
 ),
),∵“特征数”是
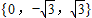 的函数图象与x轴交于点E,
的函数图象与x轴交于点E,∴函数解析式为:y=

∴图象与x、y轴分别点E(1,0)、D(0,
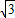 ),
),∴OD=
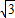 ,OC=3,OD=1.
,OC=3,OD=1.∴OD2=OC×OE,
∴△ODC∽△OED.
点评:此题主要考查了二次函数的综合应用,结合“特征数”的定义考查一次函数,二次函数的综合应用,综合性强,能力要求高.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 定义{a,b,c}为函数y=ax2+bx+c的“特征数”.如:函数y=x2-2x+3的“特征数”是{1,-2,3},函数y=2x+3的“特征数”是{0,2,3},函数y=-x的“特征数”是{0,-1,0}
定义{a,b,c}为函数y=ax2+bx+c的“特征数”.如:函数y=x2-2x+3的“特征数”是{1,-2,3},函数y=2x+3的“特征数”是{0,2,3},函数y=-x的“特征数”是{0,-1,0}