题目内容
【题目】如图1,有一组平行线l1∥l2∥l3∥l4,正方形ABCD的四个顶点分别在l1,l2,l3,l4上,EG过点D且垂直l1于点E,分别交l2,l4于点F,G,EF=DG=1,DF=2.
(1)AE=__________,正方形ABCD的边长=__________;
(2)如图2,将∠AEG绕点A顺时针旋转得到∠AE′D′,旋转角为α(0°<α<90°),点D′在直线l3上,以AD′为边在E′D′左侧作菱形AB′C′D′,使B′、C′分别在直线l2,l4上.
①写出∠B′AD′与α的数量关系并给出证明;
②若α=30°,直接写出菱形AB′C′D′的边长为__________.
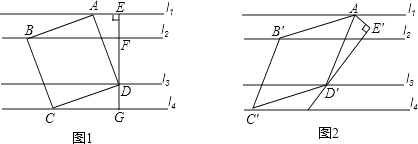
【答案】(1)1;![]() (2)①∠B'AD'=90°-α;(3)
(2)①∠B'AD'=90°-α;(3)![]()
【解析】分析:
(1)如下图1,由图结合已知条件可证得△AED≌△DGC,由此即可得到AE=DG=1;
(2)①如下图2,过点B′作B′M垂直于l1于点M,通过证Rt△AED′≌Rt△B′MA可得∠D′AE+∠B′AM=90°,由此可得∠B′AD′+α=90°,即∠B′AD′=90°-α;
②如下图2,由l1∥l2∥l3可过点E′作E′O⊥l1于点O,E′O⊥l3于点N,当α=30°时,易得OE=![]() AE=
AE=![]() ,∠D′EN=30°,结合ON=3可得EN=
,∠D′EN=30°,结合ON=3可得EN=![]() ,由此易得D′E=
,由此易得D′E=![]() ,这样在Rt△AD′E中即可由勾股定理求得AD′的长.
,这样在Rt△AD′E中即可由勾股定理求得AD′的长.
详解:
(1)如下图1,由题意可得∠AEF=∠ADC=∠CGD=90°,
∴∠1+∠2=90°,∠1+∠3=90°,
∴∠2=∠3,
又∵AD=CD,
∴△AED≌△DGC,
∴AE=DG=1,
又∵DE=EF+FD=1+2=3,
∴AD=![]() ,即正方形ABCD的边长为
,即正方形ABCD的边长为![]() ;
;
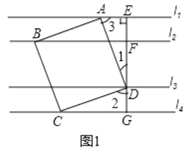
(2)①∠B′AD′=90°-α;理由如下:
如下图2,过点B′作B′M垂直于l1于点M,
∴∠B′MA=∠D′EA=90°,
由(1)可知MB′=AE=1,又∵AB′=ED′,
∴Rt△AED′≌Rt△B′MA,
∴∠B′AM=∠AD′E,
又∵∠D′AE+∠AD′E=90°,
∴∠D′AE+∠B′AM=90°,
∴∠B′AD′+α=90°,即∠B′AD′=90°-α;
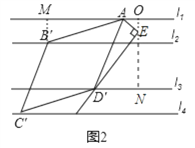
(3)如上图2,由由l1∥l2∥l3可过点E′作E′O⊥l1于点O,E′O⊥l3于点N,
∵α=30°,
∴OE==![]() AE=
AE=![]() ,∠D′EN=30°,
,∠D′EN=30°,
又∵ON=3,
∴EN=![]() ,
,
∴在Rt△D′EN中,D′E=![]() ,
,
∴在Rt△AD′E中,AD′=![]() ,
,
即菱形AB′C′D′的边长为![]() .
.

 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案