题目内容
【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若OA2=4,则△AnBnAn+1的边长为 .
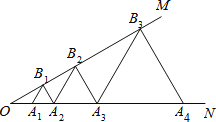
【答案】2n﹣1
【解析】
试题分析:根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3,以及A2B2=2B1A2,得出A3B3=4B1A2=8,A4B4=8B1A2=16,A5B5=16B1A2…进而得出答案.
解:∵△A1B1A2是等边三角形,
∴A1B1=A2B1,
∵∠MON=30°,
∵OA2=4,
∴OA1=A1B1=2,
∴A2B1=2,
∵△A2B2A3、△A3B3A4是等边三角形,
∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,
∴A2B2=2B1A2,B3A3=2B2A3,
∴A3B3=4B1A2=8,
A4B4=8B1A2=16,
A5B5=16B1A2=32,
以此类推△AnBnAn+1的边长为 2n﹣1.
故答案为:2n﹣1.

练习册系列答案
相关题目
【题目】甲、乙两辆汽车同时分别从A、B两城沿同一条高速公路匀速驶向C城.已知A、C两城的距离为360km,B、C两城的距离为320km,甲车比乙车的速度快10km/h,结果两辆车同时到达C城.设乙车的速度为xkm/h.
(1)根据题意填写下表:
行驶的路程(km) | 速度(km/h) | 所需时间(h) | |
甲车 | 360 |
|
|
乙车 | 320 | x |
|
(2)求甲、乙两车的速度.