题目内容
【题目】已知:直线AB与直线CD相交于点O,∠BOC=45°,
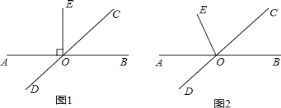
(1)如图1,若EO⊥AB,求∠DOE的度数;
(2)如图2,若EO平分∠AOC,求∠DOE的度数.
【答案】(1)135°;(2)112.5°
【解析】
试题分析:(1)根据对顶角相等求∠AOD,由垂直的性质求∠AOE,根据∠DOE=∠AOD+∠AOE求解;
(2)由邻补角的性质求∠AOC,根据EO平分∠AOC求∠AOE,再由∠DOE=∠AOD+∠AOE求解.
解:(1)∵直线AB与直线CD相交,
∴∠AOD=∠BOC=45°.
∵EO⊥AB,
∴∠AOE=90°,
∴∠DOE=∠AOD+∠AOE=135°;
(2)∵直线AB与直线CD相交,
∴∠AOD=∠BOC=45°,∠AOC=135°,
∵EO平分∠AOC,
∴∠AOE=![]() ∠AOC=67.5°,
∠AOC=67.5°,
∴∠DOE=∠AOD+∠AOE=112.5°.

练习册系列答案
相关题目
【题目】我市某草莓种植农户喜获丰收,共收获草莓2000kg.经市场调查,可采用批发、零售两种销售方式,这两种销售方式每kg草莓的利润如下表:
销售方式 | 批发 | 零售 |
利润(元/kg) | 6 | 12 |
设按计划全部售出后的总利润为y元,其中批发量为xkg.
(1)求y与x之间的函数关系式;
(2)若零售量不超过批发量的4倍,求该农户按计划全部售完后获得的最大利润.