题目内容
已知一直线与直角坐标系中两数轴交于点M（0，-3）和点N（a，0）两点，且此直线与两坐标轴围成的三角形面积为12，则a的值为（ ）
分析：根据M与N点坐标得到OM=3，ON=|a|，然后根据三角形面积公式得到
×3×|a|=12，再解方程即可．
| 1 |
| 2 |
解答：解：∵点M（0，-3）和点N（a，0），
∴OM=3，ON=|a|，
∴S△OMN=
•OM•ON=12，
∴
×3×|a|=12，
∴a=±8．
故选C．
∴OM=3，ON=|a|，
∴S△OMN=
| 1 |
| 2 |
∴
| 1 |
| 2 |
∴a=±8．
故选C．
点评：本题考查了三角形的面积：三角形面积公式=
×底×底边上的高．也考查了坐标与图形性质．
| 1 |
| 2 |
练习册系列答案
相关题目
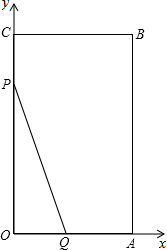已知：在平面直角坐标系中矩形OABC如图，且A（6，0）、C（0，10），P点从C出发沿折线COA匀速运动、Q点从O出发沿折线OAB匀速运动，P、Q两点同时出发运动t秒，且速度均为每秒2个单位长度，设S△OPQ=S．