题目内容
已知:在平面直角坐标系中,抛物线y=ax2-x+3(a≠0)交x轴于A、B两点,交y轴于点C,且对称轴为直线x=-2.(1)求该抛物线的解析式及顶点D的坐标;
(2)若点P(0,t)是y轴上的一个动点,请进行如下探究:
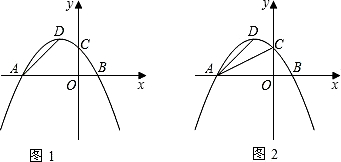
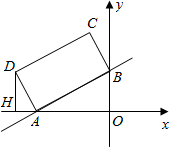
探究一:如图1,设△PAD的面积为S,令W=t•S,当0<t<4时,W是否有最大值?如果有,求出W的最大值和此时t的值;如果没有,说明理由;
探究二:如图2,是否存在以P、A、D为顶点的三角形与Rt△AOC相似?如果存在,求点P的坐标;如果不存在,请说明理由.(参考资料:抛物线y=ax2+bx+c(a≠0)对称轴是直线x=-
| b | 2a |
分析:(1)由抛物线的对称轴求出a,就得到抛物线的表达式了;
(2))①下面探究问题一,由抛物线表达式找出A,B,C三点的坐标,作DM⊥y轴于M,再由面积关系:SPAD=S梯形OADM-SAOP-SDMP得到t的表达式,从而W用t表示出来,转化为求最值问题.
②难度较大,运用分类讨论思想,可以分三种情况:
(1)当∠P1DA=90°时;(2)当∠P2AD=90°时;(3)当AP3D=90°时;思路搞清晰问题就好解决了.
(2))①下面探究问题一,由抛物线表达式找出A,B,C三点的坐标,作DM⊥y轴于M,再由面积关系:SPAD=S梯形OADM-SAOP-SDMP得到t的表达式,从而W用t表示出来,转化为求最值问题.
②难度较大,运用分类讨论思想,可以分三种情况:
(1)当∠P1DA=90°时;(2)当∠P2AD=90°时;(3)当AP3D=90°时;思路搞清晰问题就好解决了.
解答:解:(1)∵抛物线y=ax2-x+3(a≠0)的对称轴为直线x=-2.
∴-
=-2,
∴a=-
,
∴y=-
x2-x+3.
∴D(-2,4).
(2)探究一:当0<t<4时,W有最大值.
∵抛物线y=-
x2-x+3交x轴于A、B两点,交y轴于点C,
∴A(-6,0),B(2,0),C(0,3),
∴OA=6,OC=3.(4分)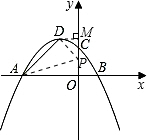
当0<t<4时,作DM⊥y轴于M,
则DM=2,OM=4.
∵P(0,t),
∴OP=t,MP=OM-OP=4-t.
∵S三角形PAD=S梯形OADM-S三角形AOP-S三角形DMP
=
(DM+OA)•OM-
OA•OP-
DM•MP
=
(2+6)×4-
×6×t-
×2×(4-t)
=12-2t(6分)
∴W=t(12-2t)=-2(t-3)2+18
∴当t=3时,W有最大值,W最大值=18.
探究二:
存在.分三种情况:
①当∠P1DA=90°时,作DE⊥x轴于E,则OE=2,DE=4,∠DEA=90°,
∴AE=OA-OE=6-2=4=DE.
∴∠DAE=∠ADE=45°,AD=
DE=4
,
∴∠P1DE=∠P1DA-∠ADE=90°-45°=45度.
∵DM⊥y轴,OA⊥y轴,
∴DM∥OA,
∴∠MDE=∠DEA=90°,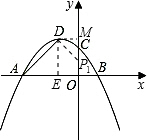
∴∠MDP1=∠MDE-∠P1DE=90°-45°=45度.
∴P1M=DM=2,P1D=
DM=2
.
此时
=
=
,
又因为∠AOC=∠P1DA=90°,
∴Rt△ADP1∽Rt△AOC,
∴OP1=OM-P1M=4-2=2,
∴P1(0,2).
∴当∠P1DA=90°时,存在点P1,使Rt△ADP1∽Rt△AOC,
此时P1点的坐标为(0,2)
②当∠P2AD=90°时,则∠P2AO=45°,
∴P2A=
=6
,
∴
=
=
.
∵
=
,
∴
≠
.
∴△P2AD与△AOC不相似,此时点P2不存在.(12分)(结论(1分),过程1分)
③当∠AP3D=90°时,以AD为直径作⊙O1,则⊙O1的半径r=
=2
,
圆心O1到y轴的距离d=4.
∵d>r,
∴⊙O1与y轴相离.
不存在点P3,使∠AP3D=90度.
∴综上所述,只存在一点P(0,2)使Rt△ADP与Rt△AOC相似.
∴-
| -1 |
| 2a |
∴a=-
| 1 |
| 4 |
∴y=-
| 1 |
| 4 |
∴D(-2,4).
(2)探究一:当0<t<4时,W有最大值.
∵抛物线y=-
| 1 |
| 4 |
∴A(-6,0),B(2,0),C(0,3),
∴OA=6,OC=3.(4分)

当0<t<4时,作DM⊥y轴于M,
则DM=2,OM=4.
∵P(0,t),
∴OP=t,MP=OM-OP=4-t.
∵S三角形PAD=S梯形OADM-S三角形AOP-S三角形DMP
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=12-2t(6分)
∴W=t(12-2t)=-2(t-3)2+18
∴当t=3时,W有最大值,W最大值=18.
探究二:
存在.分三种情况:
①当∠P1DA=90°时,作DE⊥x轴于E,则OE=2,DE=4,∠DEA=90°,
∴AE=OA-OE=6-2=4=DE.
∴∠DAE=∠ADE=45°,AD=
| 2 |
| 2 |
∴∠P1DE=∠P1DA-∠ADE=90°-45°=45度.
∵DM⊥y轴,OA⊥y轴,
∴DM∥OA,
∴∠MDE=∠DEA=90°,

∴∠MDP1=∠MDE-∠P1DE=90°-45°=45度.
∴P1M=DM=2,P1D=
| 2 |
| 2 |
此时
| OC |
| P1D |
| OA |
| AD |
3
| ||
| 4 |
又因为∠AOC=∠P1DA=90°,
∴Rt△ADP1∽Rt△AOC,
∴OP1=OM-P1M=4-2=2,
∴P1(0,2).
∴当∠P1DA=90°时,存在点P1,使Rt△ADP1∽Rt△AOC,
此时P1点的坐标为(0,2)
②当∠P2AD=90°时,则∠P2AO=45°,
∴P2A=
| OA |
| cos45° |
| 2 |
∴
| P2A |
| OA |
6
| ||
| 6 |
| 2 |
∵
| AD |
| OC |
4
| ||
| 3 |
∴
| AD |
| OC |
| P2A |
| OA |
∴△P2AD与△AOC不相似,此时点P2不存在.(12分)(结论(1分),过程1分)
③当∠AP3D=90°时,以AD为直径作⊙O1,则⊙O1的半径r=
| AD |
| 2 |
| 2 |
圆心O1到y轴的距离d=4.
∵d>r,
∴⊙O1与y轴相离.
不存在点P3,使∠AP3D=90度.
∴综上所述,只存在一点P(0,2)使Rt△ADP与Rt△AOC相似.
点评:此题综合性较强,考查函数基本性质,三角形相似的性质,辅助线的作法,探究性问题,还运用分类讨论思想,难度大.

练习册系列答案
相关题目
 如图,在平面直角坐标中,已知直线y=kx+b与直线
如图,在平面直角坐标中,已知直线y=kx+b与直线 如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数
如图,在平面直角坐标xOy中,已知点A(-5,0),P是反比例函数