题目内容
【题目】如图,直线y=﹣x+4分别交x轴、y轴于A、C两点,抛物线y=﹣x2+mx+4经过点A,且与x轴的另一个交点为点B.连接BC,过点C作CD∥x轴交抛物线于点D

(1)求抛物线的函数表达式;
(2)若点E是抛物线上的点,求满足∠ECD=∠BCO的点E的坐标;
(3)点M在y轴上且位于点C上方,点N在直线AC上,点P为第一象限内的抛物线上一点,若以点C、M、N、P为顶点的四边形是菱形,求菱形的边长.
【答案】(1)y=﹣x2+3x+4;(2)E的坐标为E![]() 或
或![]() ;(3)4
;(3)4![]() ﹣2或
﹣2或![]() .
.
【解析】
(1)利用直线方程求得点A、C的坐标,根据点A、C坐标求得抛物线解析式;
(2)分点E在CD上方、点E在CD下方两种情况,分别求解即可;
(3)分CM为菱形的一条边、CM为菱形的对角线两种情况,分别求解即可.
解:(1)y=﹣x+4,令x=0,则y=4,令y=0,则x=4,

则点A、C的坐标分别为(4,0)、(0,4),
将点A的坐标代入抛物线的表达式并解得:m=3,
故抛物线的表达式为:y=﹣x2+3x+4①,
令y=0,则x=﹣1或4,故点B(﹣1,0);
(2)①当点E在CD上方时,

tan∠BCO=![]() ,
,
则直线CE的表达式为:y=![]() x+4②,
x+4②,
联立①②并解得:x=0或![]() (舍去0),
(舍去0),
则点E(![]() ,
,![]() );
);
②当点E在CD下方时,
同理可得:点E′(![]() ,
,![]() );
);
故点E的坐标为E(![]() ,
,![]() )或(
)或(![]() ,
,![]() );
);
(3)①如图2,当CM为菱形的一条边时,
过点P作PQ∥x轴,∵OA=OC=4,
∴∠PMQ=∠CAO=45°,
设点P(x,﹣x2+3x+4),
则PM=![]() PQ=
PQ=![]() x,
x,
C、M、N、P为顶点的四边形是菱形,则PM=PN,
即:![]() x=﹣x2+3x+4,解得:x=0或4﹣
x=﹣x2+3x+4,解得:x=0或4﹣![]() (舍去0),
(舍去0),
故菱形边长为![]() x=4
x=4![]() ﹣2;
﹣2;
②如图3,当CM为菱形的对角线时,
同理可得:菱形边长为2![]() ;
;
故:菱形边长为4![]() ﹣2或
﹣2或![]() .
.

【题目】某乡镇实施产业扶贫,帮助贫困户承包了荒山种植某种苹果到了收获季节,投入市场销售时,调查市场行情,发现该苹果的销售不会亏本,且该产品的日销售量y(千克)与销售单价x(元)之间满足一次函数关系关于销售单价、日销售量、日销售利润的几组对应值如表:
销售单价x(元) | 10 | 15 | 23 | 28 |
日销售量y(千克) | 200 | 150 | 70 | m |
日销售利润w(元) | 400 | 1050 | 1050 | 400 |
(注:日销售利润=日销售量×(销售单价﹣成本单价))
(1)求y关于x的函数解析式(要写出x的取值范围)及m的值;
(2)根据以上信息,填空:产品的成本单价是 元,当销售单价x= 元时,日销售利润w最大,最大值是 元;
(3)某农户今年共采摘苹果4800千克,该品种苹果的保质期为40天,根据(2)中获得最大利润的方式进行销售,能否销售完这批苹果?请说明理由
【题目】某中学为了科学建设“学生健康成长工程”.随机抽取了部分学生家庭对其家长进行了主题为“周末孩子在家您关心吗?”的问卷调查,将回收的问卷进行分析整理,得到了如下的样本统计表和扇形统计图:
代号 | 情况分类 | 家庭数 |
| 带孩子玩并且关心其作业完成情况 | 16 |
| 只关心其作业完成情况 | b |
| 只带孩子玩 | 8 |
| 既不带孩子玩也不关心其作业完成情况 | d |
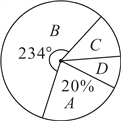
(1)求![]() 的值;
的值;
(2)该校学生家庭总数为500,学校决定按比例在![]() 类家庭中抽取家长组成培训班,其比例为
类家庭中抽取家长组成培训班,其比例为![]() 类取20%,
类取20%,![]() 类各取60%,请你估计该培训班的家庭数;
类各取60%,请你估计该培训班的家庭数;
(3)若在![]() 类家庭中只有一个城镇家庭,其余是农村家庭,请用列举法求出在
类家庭中只有一个城镇家庭,其余是农村家庭,请用列举法求出在![]() 类中随机抽出2个家庭进行深度采访,其中有一个是城镇家庭的概率.
类中随机抽出2个家庭进行深度采访,其中有一个是城镇家庭的概率.