题目内容
【题目】在平面直角坐标系 xOy中，对于点P（x，y），以及两个无公共点的图形W1和W2 ， 若在图形W1和W2上分别存在点M （x1 ， y1 ）和N （x2 ， y2 ），使得P是线段MN的中点，则称点M 和N被点P“关联”，并称点P为图形W1和W2的一个“中位点”，此时P，M，N三个点的坐标满足x= 
，y= 
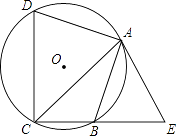
（1）已知点A（0，1），B（4，1），C（3，﹣1），D（3，﹣2），连接AB，CD．
①对于线段AB和线段CD，若点A和C被点P“关联”，则点P的坐标为；
②线段AB和线段CD的一“中位点”是Q （2，﹣ 
），求这两条线段上被点Q“关联”的两个点的坐标；
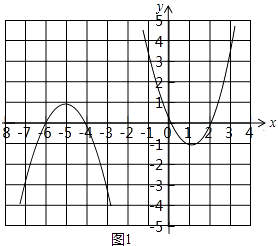
（2）如图1，已知点R（﹣2，0）和抛物线W1：y=x2﹣2x，对于抛物线W1上的每一个点M，在抛物线W2上都存在点N，使得点N和M 被点R“关联”，请在图1 中画出符合条件的抛物线W2；
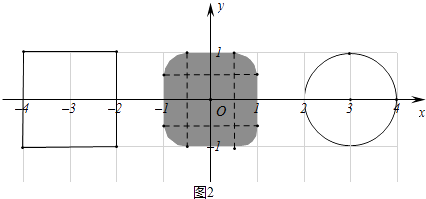
（3）正方形EFGH的顶点分别是E（﹣4，1），F（﹣4，﹣1），G（﹣2，﹣1），H（﹣2，1），⊙T的圆心为T（3，0），半径为1．请在图2中画出由正方形EFGH和⊙T的所有“中位点”组成的图形（若涉及平面中某个区域时可以用阴影表示），并直接写出该图形的面积．
【答案】
（1）（ 
，0）
（2）
解：所求作的抛物线如图1所示，
（3）
解：正方形EFGH和⊙T的所有“中位点”组成的图形如图2所示（影阴部分包括边界），
S阴=2×2﹣4[ 
× ﹣ 
π（ ）2]=3+ 
【解析】解：（1）①∵点A和C被点P“关联”，
又∵ 
= ， 
=0，
∴点P坐标（ ，0），
所以答案是（ ，0）．
②设在线段AB和线段CD上分别存在K（x，1）和L（3，y）被点Q（2，﹣ ）“关联”，则点Q是KL中点，
∴2= 
，﹣ = 
，
∴x=1，y=﹣2，
∴这两条线段上被点Q“关联”的两个点的坐标分别是（1，1）和（3，﹣2）．
