��Ŀ����
����Ŀ���ڵ���ֱ��������ABC�У�AB=AC����BAC=90�㣮��PΪֱ��AB��һ�����㣨��P�����A��B�غϣ�������PC����D��ֱ��BC�ϣ���PD=PC������P��PE^PC����D��E��ֱ��AC��ͬ�࣬��PE=PC������BE��
��1�����һ������P���߶�AB��ʱ��ͼ����ͼ1 ��ʾ��
���������ͼ2������P��BA���ӳ����ϣ���AP��ABʱ���������ⲹȫͼ2����
��2��������⣨1������������У���ѡһ�����������������⣺
����֤����ACP=��DPB��
���õ�ʽ��ʾ�߶�BC��BP��BE֮���������ϵ����֤����
���𰸡�
��1��
�⣺��ȫͼ����ͼ����ʾ

��2��
�⣺���һ��
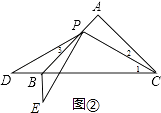
��֤������ͼ�ڣ�
��AB=AC����BAC=90�㣬
���ABC=��ACB=45�㣬
��PD=PC��
���1=��D��
�ߡ�ACB=��1+��2=45�㣬��ABC=��D+��=45�㣬
���3=��2��
����ACP=��DPB��
��BC= ![]() BP+BE�����ɣ�
BP+BE�����ɣ�
֤������ͼ�۹�P��PF��PB��BC��F��
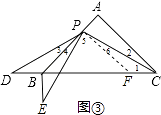
��PF��PB��
���BPF=90�㣬
��EP��PC��
���EPC=90�㣬
���4+��5=��6+��5��
���4=��6��
�ߡ�PBF=45�㣬
���PBF=��PFB=45�㣬
��PB=PF��
�ڡ�PBE���PFC�У�
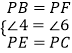 ��
��
���PBE�ա�PFC��
��BE=FC��
��BF= ![]() BP��
BP��
��BC=BF+FC= ![]() BP+BE��
BP+BE��
�����������ͼ�ܣ�
��PD=PC��
���PDC=��PCD��
�ߡ�ABC=��ACB=45�㣬
���3=��PDC��45�㣬��ACP=��PCD��45��
�����BPD=��ACP��
����ͼ�ܣ���P��PF��PB��BC��F��
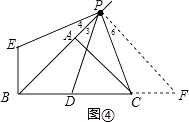
��PF��PB��
���BPF=90�㣬
��EP��PC��
���EPC=90�㣬
���4+��BPC=��6+��BPC=90�㣬
���4=��6��
�ߡ�PBF=45�㣬
���PBF=��PFB=45�㣬
��PB=PF��
�ڡ�PBE���PFC�У�
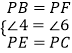 ��
��
���PBE�ա�PFC��
��BE=FC��
��BF= ![]() BP��
BP��
��BC=BF��FC= ![]() BP��BE��
BP��BE��
����������1���������ⲹȫͼ�μ��ɣ���2�����һ���ٸ��ݵ���ֱ�������ε����ʵõ���ABC=��ACB=45�㣬�ɵ��������ε����ʵõ���1=��D���������ε���ǵ����ʼ��ɵõ����ۣ��ڸ�����ǵ����ʵõ���4=��6���ɵ���ֱ�������ε����ʵõ���PBF=��PFB=45�㣬���ǵõ�PB=PF������ȫ�������ε����ʵõ�BE=FC���ɹ��ɶ����õ�BF= ![]() BP�����ɵõ����ۣ�
BP�����ɵõ����ۣ�
��������٣����ݵ��������ε����ʵõ���PDC=��PCD���ɡ�ABC=��ACB=45�㣬���ǵõ���3=��PDC��45�㣬��ACP=��PCD��45�㣬���ɵõ����ۣ�������ǵ����ʵõ���4=��6�����ݵ���ֱ�������ε����ʵõ���PBF=��PFB=45�㣬���ǵõ�PB=PF������ȫ�������ε����ʵõ�BE=FC�����ݹ��ɶ����õ�BF= ![]() BP���ǵõ����ۣ�
BP���ǵõ����ۣ�

 ��ѧ����ϵ�д�
��ѧ����ϵ�д� �ο�������ϵ�д�
�ο�������ϵ�д�


