题目内容
【题目】已知△ABC中,
(1)点O在线段AB上,以点O为圆心,AO为半径作⊙O,⊙O经过点C。
(要求尺规作图,保留作图痕迹,写结论,不必写作法。)
(2)若∠A=25°,∠B=40°,请判断BC与⊙O的位置关系并写出证明过程。

【答案】(1)作图见解析;(2)理由见解析.
【解析】试题分析:(1)利用基本作图(作已知线段的垂直平分线)作线段AB的垂直平分线l;
(2)连结OC,如图,根据线段垂直平分线的性质得∠A=∠OCA=25°,再利用三角形外角性质得∠BOC=50°,接着根据三角形内角和可计算出∠BCO=90°,然后根据切线的判定定理即可判断BC为⊙O的切线.
试题解析:(1)如图,直线l为所求;
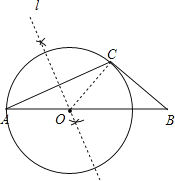
(2)⊙O为所求.
BC与⊙O相切.理由如下:
连结OC,如图,
∵直线l垂直平分AC,
∴∠A=∠OCA=25°,
∴∠BOC=∠A+∠OCA=50°,
∵∠B=40°,
∴∠BCO=180°﹣∠BOC﹣∠B=90°,
∴OC⊥BC,
∴BC为⊙O的切线.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目