题目内容
【题目】如图1,在△ABC中,∠ACB=90°,BC=2,∠A=30°,点E,F分别是线段BC,AC的中点,连结EF.
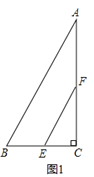
(1)![]() = .
= .
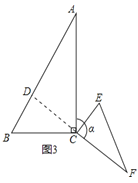
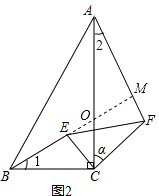
(2)如图2,当△CEF绕点C顺时针旋转a时(0°<a<180°),连结AF,BE,求线段BE与线段AF的位置关系和![]() 。
。

(3)如图3,当△CEF绕点C顺时针旋转a时(0°<a<180°),延长FC交AB于点D,如果AD=6﹣2![]() ,求旋转角a的度数.
,求旋转角a的度数.
【答案】(1)![]() ;(2)证明见解析;(3)135°.
;(2)证明见解析;(3)135°.
【解析】试题分析:(1)结合已知角度以及利用锐角三角函数关系求出AB的长,进而得出答案;
(2)利用已知得出△BEC∽△AFC,进而得出∠1=∠2,即可得出答案;
(3)过点D作DH⊥BC于H,则DB=4-(6-2![]() )=2
)=2![]() -2,进而得出BH=
-2,进而得出BH=![]() -1,DH=3-
-1,DH=3-![]() ,求出CH=BH,得出∠DCA=45°,进而得出答案.
,求出CH=BH,得出∠DCA=45°,进而得出答案.
试题解析:(1)如图1,线段BE与AF的位置关系是互相垂直;
∵∠ACB=90°,BC=2,∠A=30°,
∴AC=2![]() ,
,
∵点E,F分别是线段BC,AC的中点,
∴![]() =
=![]()
(2))如图2,∵点E,F分别是线段BC,AC的中点,
∴EC=![]() BC,FC=
BC,FC=![]() AC,
AC,
∴![]() ,
,
∵∠BCE=∠ACF=α,
∴△BEC∽△AFC,
∴![]() ,
,
∴∠1=∠2,
延长BE交AC于点O,交AF于点M
∵∠BOC=∠AOM,∠1=∠2
∴∠BCO=∠AMO=90°
∴BE⊥AF;
(3)如图3,
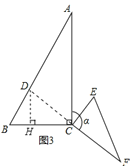
∵∠ACB=90°,BC=2,∠A=30°∴AB=4,∠B=60°
过点D作DH⊥BC于H∴DB=4-(6-2![]() )=2
)=2![]() -2,
-2,
∴BH=![]() -1,DH=3-
-1,DH=3-![]() ,又∵CH=2-(
,又∵CH=2-(![]() -1)=3-
-1)=3-![]() ,
,
∴CH=BH,∴∠HCD=45°,∴∠DCA=45°,α=180°-45°=135°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目



