题目内容
【题目】菱形OABC在平面直角坐标系中的位置如图所示顶点A（5,0），OB=
，P是对角线OB上的一个动点，D（0,1），当CP+DP的值最小时，点P的坐标为（ ）
A. (
，3
) B. （
，
） C. （1，
） D. （
，）
【答案】B
【解析】分析：如图连接AC，AD，分别交OB于G、P，作BK⊥OA于K．首先说明点P就是所求的点，再求出点B坐标，求出直线OB、DA，列方程组即可解决问题．
详解：如图连接AC，AD，分别交OB于G、P，作BK⊥OA于K．
∵四边形OABC是菱形，
∴AC⊥OB，GC=AG，OG=BG=2
，
∵A、C关于直线OB对称，
∴PC+PD=PA+PD=DA，
∴此时PC+PD最短，
在RT△AOG中，AG=
=
，
∴AC=2，
∵OABK=
ACOB，
∴BK=4，AK=
=3，
∴点B坐标（8，4），
∴直线OB解析式为y=x，直线AD解析式为y=-
x+1，
由
，
解得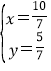
，
∴点P坐标（
，
）．
故选B．
练习册系列答案
相关题目
【题目】近两年，国际市场黄金价格涨幅较大，中国交通银行推出“沃德金”的理财产品，即以黄金为投资产品，投资者从黄金价格的上涨中赚取利润．上周五黄金的收盘价为285元/克，下表是本周星期一至星期五黄金价格的变化情况．（注：星期一至星期五开市，星期六.星期日休市）
星期 | 一 | 二 | 三 | 四 | 五 |
收盘价的变化（与前一天收盘价比较） | +7 | +5 |
|
| +8 |
问：（1）本周星期三黄金的收盘价是多少？
（2）本周黄金收盘时的最高价.最低价分别是多少？
（3）上周，小王以周五的收盘价285元/克买入黄金1000克，已知买入与卖出时均需支付成交金额的千分之五的交易费，卖出黄金时需支付成交金额的千分之三的印花税．本周，小王以周五的收盘价全部卖出黄金1000克，他的收益情况如何？
