题目内容
 如图所示,在直角坐标系中放置一个边长为1的正方形ABCD,将正方形ABCD沿x轴的正方向无滑动的在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径线与x轴围成的面积为
如图所示,在直角坐标系中放置一个边长为1的正方形ABCD,将正方形ABCD沿x轴的正方向无滑动的在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径线与x轴围成的面积为π+1
π+1
.分析:根据旋转的性质作出图形,再利用勾股定理列式求出正方形的对角线,然后根据点A运动的路径线与x轴围城的面积为三个扇形的面积加上两个直角三角形的面积,列式计算即可得解.
解答: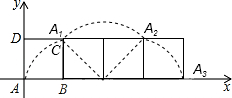 解:如图,∵正方形ABCD的边长为1,
解:如图,∵正方形ABCD的边长为1,
∴对角线长:
=
,
点A运动的路径线与x轴围成的面积为:
+
+
+
×1×1+
×1×1
=
π+
π+
π+
+
=π+1.
故答案为:π+1.
 解:如图,∵正方形ABCD的边长为1,
解:如图,∵正方形ABCD的边长为1,∴对角线长:
| 12+12 |
| 2 |
点A运动的路径线与x轴围成的面积为:
| 90•π•12 |
| 360 |
90•π•
| ||
| 360 |
| 90•π•12 |
| 360 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
=π+1.
故答案为:π+1.
点评:本题考查了旋转的性质,正方形的性质,扇形的面积,读懂题意并作出图形,观察出所求面积的组成部分是解题的关键,作出图形更形象直观.

练习册系列答案
相关题目
 sin∠BOA=
sin∠BOA= 1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.
1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.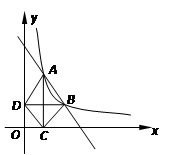

 的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.
的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连接AD、DC、CB.