��Ŀ����
����Ŀ����ͼ��������y=![]() ��x�ύ�ڵ�A����B����y�ύ�ڵ�C����D���C����x��Գƣ���P��x���ϵ�һ�����㣬���P������Ϊ��m��0��������P��x��Ĵ���l���������ڵ�Q��
��x�ύ�ڵ�A����B����y�ύ�ڵ�C����D���C����x��Գƣ���P��x���ϵ�һ�����㣬���P������Ϊ��m��0��������P��x��Ĵ���l���������ڵ�Q��
��1�����A����B����C�����ꣻ
��2����ֱ��BD�Ľ���ʽ��
��3������P���߶�OB���˶�ʱ��ֱ��l��BD�ڵ�M����̽��mΪ��ֵʱ���ı���CQMD��ƽ���ı��Σ�
��4���ڵ�P���˶������У��Ƿ���ڵ�Q��ʹ��BDQ����BDΪֱ�DZߵ�ֱ�������Σ������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�

���𰸡���1��A����1��0����B��4��0����C��0��2������2��![]() ����3��m=2����4��Q������Ϊ��3��2������8����18��������1��0����
����3��m=2����4��Q��������3��2������8����18��������1��0����
��������
���⣨1�����ݺ�������ʽ�з��̼��ɵõ����ۣ�
��2���ɵ�C���D����x��Գƣ��õ�D��0����2�����ⷽ�̼��ɵõ����ۣ�
��3����ͼ1��ʾ������ƽ���ı��ε����ʵõ�QM=CD�����Q������Ϊ��m��![]() ������M��m��
������M��m��![]() �����з��̼��ɵõ����ۣ�
�����з��̼��ɵõ����ۣ�
��4�����Q������Ϊ��m��![]() ���������������������QBD=90��ʱ�����ݹ��ɶ����з������m=3��m=4���������⣬��ȥ����������QDB=90��ʱ�����ݹ��ɶ����з������m=8��m=��1�����ǵõ����ۣ�
���������������������QBD=90��ʱ�����ݹ��ɶ����з������m=3��m=4���������⣬��ȥ����������QDB=90��ʱ�����ݹ��ɶ����з������m=8��m=��1�����ǵõ����ۣ�
�����������1������x=0�ã�y=2����C��0��2����
����y=0�ã�![]() ����ã�
����ã�![]() ��
��![]() ����A����1��0����B��4��0����
����A����1��0����B��4��0����
��2������C���D����x��Գƣ���D��0����2����
��ֱ��BD�Ľ���ʽΪy=kx��2��
������4��0������ã�4k��2=0����k=![]() ����ֱ��BD�Ľ���ʽΪ
����ֱ��BD�Ľ���ʽΪ![]() ��
��
��3����ͼ1��ʾ��
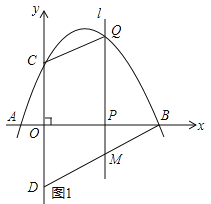
��QM��DC������QM=CDʱ���ı���CQMD��ƽ���ı��Σ�
���Q��������m��![]() ������M��m��
������M��m��![]() ������
������![]() ����ã�m=2��m=0���������⣬��ȥ��������m=2ʱ���ı���CQMD��ƽ���ı��Σ�
����ã�m=2��m=0���������⣬��ȥ��������m=2ʱ���ı���CQMD��ƽ���ı��Σ�
��4�����ڣ����Q������Ϊ��m��![]() �����ߡ�BDQ����BDΪֱ�DZߵ�ֱ�������Σ���������������ۣ�
�����ߡ�BDQ����BDΪֱ�DZߵ�ֱ�������Σ���������������ۣ�
������QBD=90��ʱ���ɹ��ɶ����ã�![]() ����
����![]() ����ã�m=3��m=4���������⣬��ȥ������Q��3��2����
����ã�m=3��m=4���������⣬��ȥ������Q��3��2����
������QDB=90��ʱ���ɹ��ɶ����ã�![]() ����
����![]() ����ã�m=8��m=��1����Q��8����18��������1��0����
����ã�m=8��m=��1����Q��8����18��������1��0����
������������Q��������3��2������8����18��������1��0����

����Ŀ�����鳬���������ס���������ɫ��װʳƷ��800�����ס���������ɫ��װʳƷ�Ľ��ۺ��ۼ��������֪����2000Ԫ�������ִ�װʳƷ����������1600Ԫ�������ִ�װʳƷ��������ͬ��
�� | �� | |
���ۣ�Ԫ/���� | m | m��2 |
�ۼۣ�Ԫ/���� | 20 | 13 |
��1����m��ֵ��
��2�����繺���ļס���������ɫ��װʳƷȫ����������������������5200Ԫ���Ҳ�����5280Ԫ���ʸó����м��ֽ����������������ۼ۩����ۣ�



