题目内容
【题目】吉祥超市准备购进甲、乙两种绿色袋装食品共800袋.甲、乙两种绿色袋装食品的进价和售价如表.已知:用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同.
甲 | 乙 | |
进价(元/袋) | m | m﹣2 |
售价(元/袋) | 20 | 13 |
(1)求m的值;
(2)假如购进的甲、乙两种绿色袋装食品全部卖出,所获总利润不少于5200元,且不超过5280元,问该超市有几种进货方案?(利润=售价﹣进价)
【答案】(1)10;(2)超市有17种进货方案
【解析】
(1)根据数量=总价÷单价结合用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同,即可得出关于m的分式方程,解之经检验后即可得出结论;
(2)设购进甲种袋装食品x袋,则购进乙种袋装食品(800﹣x)袋,根据总利润=每袋的利润×购进数量结合所获总利润不少于5200元且不超过5280元,即可得出关于x的一元一次不等式组,解之即可得出x的取值范围,结合x为正整数即可得出该超市有17种进货方案.
(1)依题意,得: ![]() ,
,
解得:m=10,
经检验,m=10是原方程的解,且符合题意.
答:m的值为10.
(2)设购进甲种袋装食品x袋,则购进乙种袋装食品(800﹣x)袋,
依题意,得: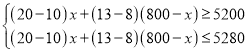 ,
,
解得:240≤x≤256.
∵x为正整数,
∴x=240,241,242,243,244,245,246,247,248,249,250,251,252,253,254,255,256.
答:该超市有17种进货方案.

练习册系列答案
相关题目





