题目内容
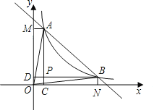
【题目】已知D是等边△ABC边AB上的一点,现将△ABC折叠,使点C与D重合,折痕为EF,点E、
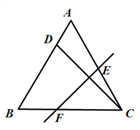
F分别在AC和BC上.如图,若AD∶DB=1∶4,则CE∶CF=________.
【答案】![]() .
.
【解析】如下图,连接DE、DF,设AD=x,则DB=4x,AB=5x,
∵△ABC是等边三角形,
∴∠A=∠B=∠ACB=60°,AB=BC=AC=5x,
由折叠的性质可知:CE=DE,CF=DF,∠EDF=∠ACB=60°,
∴∠BDF+∠BFD=180°-60°=120°,∠BDF+∠ADE=180°-∠EDF=120°,
∴∠BFD=∠ADE,
∴△ADE∽△BFD,
∴DE:DF=△ADE的周长:△BDF的周长,
∵△AED的周长=AD+DE+AE=AD+AC=6x,△BDF的周长BD+BF+DF=BD+BC=9x,
∴DE:DF=5x:7x=2:3.
故答案为:2:3.


练习册系列答案
相关题目