题目内容
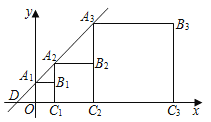
【题目】直线y=x+1与x轴交于点D,与y轴交于点A1,把正方形A1B1C1O1、A2B2C2C1和A3B3C3C2按如图所示方式放置,点A2、A3在直线y=x+1上,点C1、C2、C3在x轴上,按照这样的规律,则正方形A2020B2020C2020C2019中的点B2020的坐标为_____.
【答案】(22020﹣1,22019)
【解析】
求出直线y=x+1与x轴、y轴的交点坐标,进而确定第1个正方形的边长,再根据等腰直角三角形的性质,得出第2个、第3个……正方形的边长,进而得出B1、B2、B3……的坐标,根据规律得到答案.
解:直线y=x+1与x轴,y轴交点坐标为:A1(0,1),即正方形OA1B1C1的边长为1,
∵△A1B1A2、△A2B2A3,都是等腰直角三角形,边长依次为1,2,4,8,16,
∴B1(1,1),B2(3,2),B3(7,4),B4(15,8),
即:B1(21﹣1,20),B2(22﹣1,21),B3(23﹣1,22),B4(24﹣1,23),
故答案为:B2020(22020﹣1,22019).

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目