Question

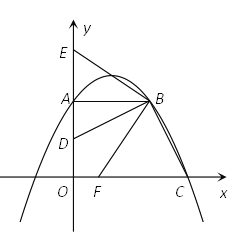
【题目】如图，已知直角梯形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，OA＝AB＝2，OC＝3，过点B作BD⊥BC，交OA于点D．将∠DBC绕点B按顺时针方向旋转，角的两边分别交y轴的正半轴、x轴的正半轴于E和F．

（1）求经过A、B、C三点的抛物线的解析式；

（2）当BE经过（1）中抛物线的顶点时，求CF的长；

（3）连结EF，设△BEF与△BFC的面积之差为S，问：当CF为何值时S最小，并求出这个最小值．

Answer 1

【答案】（1）y=﹣+x+2；（2）；（3）当a=2（在0＜a＜3范围内）时，S最小值=．

【解析】试题分析：（1）根据OA、AB、OC的长，即可得到A、B、C三点的坐标，进而可用待定系数法求出抛物线的解析式；

（2）此题要通过构造全等三角形求解；过B作BM⊥x轴于M，由于∠EBF是由∠DBC旋转而得，所以这两角都是直角，那么∠EBF=∠ABM=90°，根据同角的余角相等可得∠EBA=∠FBM；易知BM=OA=AB=2，由此可证得△FBM≌△EBA，则AE=FM；CM的长易求得，关键是FM即AE的长；设抛物线的顶点为G，由于G点在线段AB的垂直平分线上，若过G作GH⊥AB，则GH是△ABE的中位线，G点的坐标易求得，即可得到GH的长，从而可求出AE的长，即可由CF=CM+FM=AE+CM求出CF的长；

（3）由（2）的全等三角形易证得BE=BF，则△BEF是等腰直角三角形，其面积为BF平方的一半；△BFC中，以CF为底，BM为高即可求出△BFC的面积；可设CF的长为a，进而表示出FM的长，由勾股定理即可求得BF的平方，根据上面得出的两个三角形的面积计算方法，即可得到关于S、a的函数关系式，根据函数的性质即可求出S的最小值及对应的CF的长．

解：（1）由题意可得A（0，2），B（2，2），C（3，0），

设所求抛物线的解析式为y=ax2+bx+c（a≠0），

则，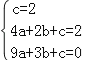

解得；

∴抛物线的解析式为y=﹣+x+2；

（2）设抛物线的顶点为G，

则G（1，），过点G作GH⊥AB，垂足为H，

则AH=BH=1，GH=﹣2=；

∵EA⊥AB，GH⊥AB，

∴EA∥GH；

∴GH是△BEA的中位线，

∴EA=2GH=；

过点B作BM⊥OC，垂足为M，则BM=OA=AB；

∵∠EBF=∠ABM=90°，

∴∠EBA=∠FBM=90°﹣∠ABF，

∴Rt△EBA≌Rt△FBM，

∴FM=EA=；

∵CM=OC﹣OM=3﹣2=1，

∴CF=FM+CM=；

（3）设CF=a，则FM=a﹣1，

∴BF2=FM2+BM2=（a﹣1）2+22=a2﹣2a+5，

∵△EBA≌△FBM，

∴BE=BF，

则S△BEF=BEBF=（a2﹣2a+5），

又∵S△BFC=FCBM=×a×2=a，

∴S=（a2﹣2a+5）﹣a=a2﹣2a+，

即S=（a﹣2）2+；

∴当a=2（在0＜a＜3范围内）时，S最小值=．