题目内容
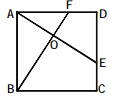
【题目】如图，每个小正方形的边长为1．
（1）求四边形ABCD的面积和周长；
（2）∠BCD是直角吗？说明理由．
【答案】（1）5
+3
+5，17.5；（2）见解析.
【解析】
（1）直接利用勾股定理得出各边长，进而利用四边形所在矩形面积减去周围三角形面积得出答案；
（2）利用勾股定理的逆定理得出答案．
（1）由勾股定理可得：AB2＝72+12＝50，
则AB＝
＝5，
∵BC2＝42+22＝20，
∴BC＝2，
∵CD2＝22+12＝5，
∴CD＝，
∵AD2＝32+42＝25，
∴AD＝5，
故四边形ABCD的周长为：5+2+5+＝5+3+5，
四边形ABCD的面积为：7×5﹣
（1×7+4×2+2×1+4×3）﹣3＝35﹣17.5＝17.5；
（2）由（1）得：BC2＝20，CD2＝5，而BD2＝32+42＝25，
故DC2+BC2＝BD2，
则∠BCD＝90°．
练习册系列答案
阅读快车系列答案
相关题目
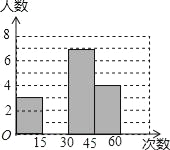
【题目】在大课间活动中，体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试，并对成绩进行统计分析，绘制了频数分布表和统计图，请你根据图表中的信息完成下列问题：
分 组 | 频数 | 频率 |
第一组（0≤x＜15） | 3 | 0.15 |
第二组（15≤x＜30） | 6 | a |
第三组（30≤x＜45） | 7 | 0.35 |
第四组（45≤x＜60） | b | 0.20 |
（1）频数分布表中a=_____，b=_____，并将统计图补充完整；
（2）如果该校七年级共有女生180人，估计仰卧起坐能够一分钟完成30或30次以上的女学生有多少人？
（3）已知第一组中只有一个甲班学生，第四组中只有一个乙班学生，老师随机从这两个组中各选一名学生谈心得体会，则所选两人正好都是甲班学生的概率是多少？
