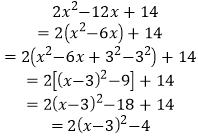题目内容
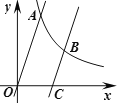
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 在直线
在直线![]() 上,点
上,点![]() 是线段
是线段![]() 上的一个动点,过点
上的一个动点,过点![]() 作
作![]() 轴交直线
轴交直线![]() 点
点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
(1)![]() 的值为 ;
的值为 ;
(2)用含有![]() 的式子表示线段
的式子表示线段![]() 的长;
的长;
(3)若![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数表达式,并求出当
之间的函数表达式,并求出当![]() 最大时点
最大时点![]() 的坐标;
的坐标;
(4)在(3)的条件下,把直线![]() 沿着
沿着![]() 轴向下平移,交
轴向下平移,交![]() 轴于点
轴于点![]() ,交线段
,交线段![]() 于点
于点![]() ,若点
,若点![]() 的坐标为
的坐标为![]() ,在平移的过程中,当
,在平移的过程中,当![]() 时,请直接写出点
时,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)7;(2)![]() ;(3)
;(3)![]()
![]() ,
,![]() ;(4)
;(4)![]()
【解析】
(1)直接把点B坐标代入y=x+2求出n的值即可;
(2)分别用m表示出点C和点P的坐标,再利用两点间距离公式求出CP的长即可;
(3)根据图形得![]() 的面积
的面积![]() 的面积,通过计算可得S
的面积,通过计算可得S![]() ,当点
,当点![]() 与点
与点![]() 重合时,
重合时,![]() 有最大值,即
有最大值,即![]() 时,
时,![]() 有最大值,将m=5代
有最大值,将m=5代![]() 求解即可;
求解即可;
(4)求出直线DM的解析,进而得出直线MN的解析式,然后把m=5代入求值即可得到结论.
(1)把点![]() 代入直线y=x+2得:n=5+2=
代入直线y=x+2得:n=5+2=![]() ,
,
故答案为:7;
(2)![]() 点
点![]() 的横坐标为
的横坐标为![]() ,
,
![]() 点
点![]() ,
,
![]() 轴交直线
轴交直线![]() 于点
于点![]() ,
,
![]() 点
点![]() ,
,
![]()
![]() ;
;
(3)![]() 直线
直线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,
![]() 点
点![]() ,
,
![]() 的面积
的面积![]() 的面积
的面积
![]()
![]()
![]()
![]()
![]()
![]() ,
,![]() 随
随![]() 的增大而增大,
的增大而增大,
![]() 点
点![]() 是线段
是线段![]() 上的一个动点,
上的一个动点,
![]() 当点
当点![]() 与点
与点![]() 重合时,
重合时,![]() 有最大值,即
有最大值,即![]() 时,
时,![]() 有最大值.
有最大值.
当![]() 时,
时,![]()
![]() 点
点![]() ;
;
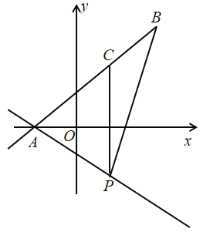
(4)如图,

∵直线![]() 沿着
沿着![]() 轴向下平移,交
轴向下平移,交![]() 轴于点
轴于点![]() ,交线段
,交线段![]() 于点
于点![]() ,
,
∴设MN所在直线解析式为:![]()
∵∠DMN=90°,
根据两条直线互相垂直,k的值互为相反数,且垂足为M,
故可设直线DM的解析式为:y=-x+b,
∵点![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,
,
解得,b=![]() ,
,
∴直线MN的解析式为:![]()
又点N的横坐标为5,
∴当x=5时,y=![]() ,
,
∴点![]() .
.

【题目】某校组织“大手拉小手,义卖献爱心”活动,计划购买黑白两种颜色的文化衫进行手绘设计后出售,并将所获利润全部捐给山区困难孩子.已知该学校从批发市场花4800元购买了 黑白两种颜色的文化衫200件,每件文化衫的批发价及手绘后的零售价如表:
批发价(元) | 零售价(元) | |
黑 色 文化衫 | 25 | 45 |
白 色 文 化 衫 | 20 | 35 |
(1)学校购进黑.白文化衫各几件?
(2)通过手绘设计后全部售出,求该校这次义卖活动所获利润.