题目内容
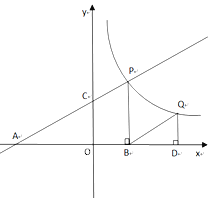
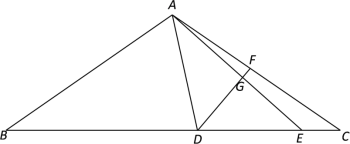
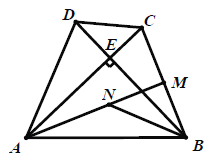
【题目】如图①,在四边形![]() 中,
中,![]() 于点
于点![]() ,
,![]() ,点
,点![]() 为
为![]() 中点,
中点,![]() 为线段
为线段![]() 上的点,且
上的点,且![]() .
.
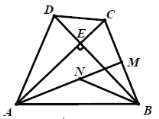
(1)求证:![]() 平分
平分![]() ;
;
(2)若![]() ,连接
,连接![]() ,当四边形
,当四边形![]() 为平行四边形时,求线段
为平行四边形时,求线段![]() 的长;
的长;
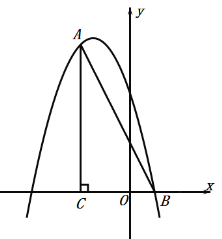
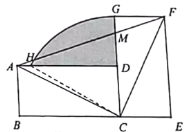
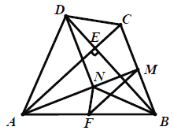
(3)若点![]() 为
为![]() 的中点,连接
的中点,连接![]() 、
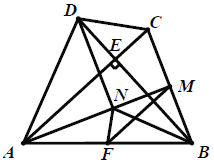
、![]() (如图②),求证:
(如图②),求证:![]() .
.
【答案】(1)详见解析;(2)![]() ;(3)详见解析.
;(3)详见解析.
【解析】
(1)由![]() 知
知![]() ,由等腰三角形三线合一知AM⊥BC,从而根据∠MAB+∠ABC=∠EBC+∠ACB知∠MAB=∠EBC,再由△MBN为等腰直角三角形知∠EBC+∠NBE=∠MAB+∠ABN=∠MNB=45°可得证;
,由等腰三角形三线合一知AM⊥BC,从而根据∠MAB+∠ABC=∠EBC+∠ACB知∠MAB=∠EBC,再由△MBN为等腰直角三角形知∠EBC+∠NBE=∠MAB+∠ABN=∠MNB=45°可得证;
(2)设BM=CM=MN=a,知DN=BC=2a,证△ABN≌△DBN得AN=DN=2a,Rt△ABM中利用勾股定理可得a的值,从而得出答案;
(3)F是AB的中点知MF=AF=BF及∠FMN=∠MAB=∠CBD,再由![]() ,即
,即![]() 得△MFN∽△BDC,即可得证.
得△MFN∽△BDC,即可得证.
解:(1)如下图所示:
∵![]() ,
,
∴![]() ,
,
∵![]() 为
为![]() 的中点,
的中点,
∴![]()
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,即
,即![]() 平分
平分![]() ;
;
(2)如下图所示:
设![]() ,
,
∵四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
∵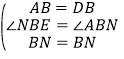 ,
,
∴![]() ≌
≌![]() (
(![]() ),
),
∴![]() ,
,
在![]() 中,由
中,由![]() 可得
可得![]() ,
,
解得:![]() (负值舍去),
(负值舍去),
∴![]() ;
;
(3)∵![]() 是
是![]() 的中点,
的中点,
∴在![]() 中,
中,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ∽
∽![]() .
.
∴![]() .
.

练习册系列答案
相关题目