Question

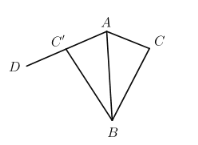
【题目】如图，在Rt△ABO中，∠ABO＝90°，其顶点O为坐标原点，点B在第二象限，点A在x轴负半轴上若BD⊥AO于点D，OB＝，AB＝2．

（1）求OA的长；

（2）求点A，B的坐标．

Answer 1

【答案】(1)5;(2) A（﹣5，0），B（﹣1，2）.

【解析】

（1）根据勾股定理求出AO即可；

（2）由AO，即可得出A的坐标；证△BDO∽△ABO，得出比例式，代入求出OD、BD，即可得出B的坐标．

解：（1）在Rt△ABO中，∠ABO＝90°，OB＝，AB＝2，

由勾股定理得：OA＝＝5，

（2）∵OA＝5，

∴A的坐标是（﹣5，0），

∵BD⊥OA，

∴∠BDO＝∠ABO＝90°，

∵∠BOD＝∠BOD，

∴△BDO∽△ABO，

∴，

∴ ，

解得：OD＝1，BD＝2，

即B的坐标是（﹣1，2），